Chapter 6: Decimals (Lecture Notes)
... Comparison of Two Decimals 1. Convert the given decimals into like decimals. 2. First compare their whole number parts. The decimal with the greater whole number part is greater. 3. If the whole number parts are equal, compare the tenths digits. The decimal with bigger digit- in tenths place is grea ...
... Comparison of Two Decimals 1. Convert the given decimals into like decimals. 2. First compare their whole number parts. The decimal with the greater whole number part is greater. 3. If the whole number parts are equal, compare the tenths digits. The decimal with bigger digit- in tenths place is grea ...
IOSR Journal of Mathematics (IOSR-JM)
... At this point it is timely to let the readers know that there are infinitely odd integers which possess more than one – may be two, three and even more, Pythagorean primitive * triplets. (4.2) For Even integers: There are some more points of clarifications when the first integer of the primitive tri ...
... At this point it is timely to let the readers know that there are infinitely odd integers which possess more than one – may be two, three and even more, Pythagorean primitive * triplets. (4.2) For Even integers: There are some more points of clarifications when the first integer of the primitive tri ...
Unit 4 The Number System: Decimals
... multi-digit numbers. Students will also multiply fractions and decimals by whole numbers. Terminology. Even though mathematically 1 is considered a power of 10 (with exponent 0), we are not introducing it as such in this section. There is some confusion in naming decimal fractions. We use the conven ...
... multi-digit numbers. Students will also multiply fractions and decimals by whole numbers. Terminology. Even though mathematically 1 is considered a power of 10 (with exponent 0), we are not introducing it as such in this section. There is some confusion in naming decimal fractions. We use the conven ...
Floating-point Arithmetic
... Positional Number System • Fixed-Point Notation: – Present a number by the positions – E.g. (101.011)2=1*22+0+1*20+0*2-1+2-2+2-3 – Difficulty occurs when presenting very large or very small numbers. – The difficulty can be overcome by scientific notation. ...
... Positional Number System • Fixed-Point Notation: – Present a number by the positions – E.g. (101.011)2=1*22+0+1*20+0*2-1+2-2+2-3 – Difficulty occurs when presenting very large or very small numbers. – The difficulty can be overcome by scientific notation. ...
Significant Figures
... higher round up, 4 or lower round down LEFT of Decimal: Replace non significant figures with zeroes if they are to the LEFT of the decimal point RIGHT of Decimal: Drop non significant figures if they are to the RIGHT of the decimal point ...
... higher round up, 4 or lower round down LEFT of Decimal: Replace non significant figures with zeroes if they are to the LEFT of the decimal point RIGHT of Decimal: Drop non significant figures if they are to the RIGHT of the decimal point ...
uncorrected page proofs
... • Decimals can be written as single fractions by using place values. Number ...
... • Decimals can be written as single fractions by using place values. Number ...
Floating point numbers in Scilab
... source code, where they are associated with double precision, that is, twice the precision of a basic real variable. The set of floating point numbers is not a continuum, it is a finite set. There are 264 ≈ 1019 different doubles in Scilab. These numbers are not equally spaced, there are holes betw ...
... source code, where they are associated with double precision, that is, twice the precision of a basic real variable. The set of floating point numbers is not a continuum, it is a finite set. There are 264 ≈ 1019 different doubles in Scilab. These numbers are not equally spaced, there are holes betw ...
fractions - MySolutionGuru
... 1. A fraction is also called a rational number. 2. A fraction is equal to zero when its numerator alone is zero. The denominator of a fraction is always assumed to be non-zero. 3. A fraction is unit when its numerator and denominator are equal. 4. The value of a fraction is not altered by multiplyin ...
... 1. A fraction is also called a rational number. 2. A fraction is equal to zero when its numerator alone is zero. The denominator of a fraction is always assumed to be non-zero. 3. A fraction is unit when its numerator and denominator are equal. 4. The value of a fraction is not altered by multiplyin ...
Floating point numbers in Scilab
... source code, where they are associated with double precision, that is, twice the precision of a basic real variable. The set of floating point numbers is not a continuum, it is a finite set. There are 264 ≈ 1019 different doubles in Scilab. These numbers are not equally spaced, there are holes betw ...
... source code, where they are associated with double precision, that is, twice the precision of a basic real variable. The set of floating point numbers is not a continuum, it is a finite set. There are 264 ≈ 1019 different doubles in Scilab. These numbers are not equally spaced, there are holes betw ...
Chapter 1 - Pearson Education
... To round 72,304 to the nearest thousand, observe that the digit in the hundreds place is 3. Since the digit is less than 5, we do not add 1 to the digit in the thousands place. The number 72,304 rounded to the nearest thousand is 72,000. ...
... To round 72,304 to the nearest thousand, observe that the digit in the hundreds place is 3. Since the digit is less than 5, we do not add 1 to the digit in the thousands place. The number 72,304 rounded to the nearest thousand is 72,000. ...
Continued Fractions
... be represented as 13 . All rational numbers can be represented as either a terminating decimal or a repeating decimal. Irrational Number: A number which cannot be represented as a simple fraction, e.g. π , which is not exactly equal to any simple fraction. When represented as decimal fractions, irra ...
... be represented as 13 . All rational numbers can be represented as either a terminating decimal or a repeating decimal. Irrational Number: A number which cannot be represented as a simple fraction, e.g. π , which is not exactly equal to any simple fraction. When represented as decimal fractions, irra ...
Floating point numbers in Scilab
... source code, where they are associated with double precision, that is, twice the precision of a basic real variable. The set of floating point numbers is not a continuum, it is a finite set. There are 264 ≈ 1019 different doubles in Scilab. These numbers are not equally spaced, there are holes betw ...
... source code, where they are associated with double precision, that is, twice the precision of a basic real variable. The set of floating point numbers is not a continuum, it is a finite set. There are 264 ≈ 1019 different doubles in Scilab. These numbers are not equally spaced, there are holes betw ...
physics_1_stuff - Humble Independent School District
... Identify the dependent and independent variables. The independent variable is the one that is intentionally changed while the dependent variable changes as a result to the alteration of the independent variable. Choose the scale you will use for the graph. Make the graph as large as possible and use ...
... Identify the dependent and independent variables. The independent variable is the one that is intentionally changed while the dependent variable changes as a result to the alteration of the independent variable. Choose the scale you will use for the graph. Make the graph as large as possible and use ...
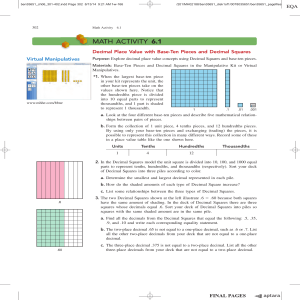
MATH ACTIVITY 6.1
... have the same amount of shading. In the deck of Decimal Squares there are three squares whose decimals equal .6. Sort your deck of Decimal Squares into piles so squares with the same shaded amount are in the same pile. a. Find all the decimals from the Decimal Squares that equal the following: .5, . ...
... have the same amount of shading. In the deck of Decimal Squares there are three squares whose decimals equal .6. Sort your deck of Decimal Squares into piles so squares with the same shaded amount are in the same pile. a. Find all the decimals from the Decimal Squares that equal the following: .5, . ...
Decimals - College of the Redwoods
... of quoting stock prices in fractions and switched to decimals. It was said that pricing stocks the same way other consumer items were priced would make it easier for investors to understand and compare stock prices. Foreign exchanges had been trading in decimals for decades. Supporters of the change ...
... of quoting stock prices in fractions and switched to decimals. It was said that pricing stocks the same way other consumer items were priced would make it easier for investors to understand and compare stock prices. Foreign exchanges had been trading in decimals for decades. Supporters of the change ...
Version 0.3
... addition, multiplication and division, and their connections to topics such as modular arithmetic, greatest common divisors, the Fast Fourier Transform (FFT), and the computation of special functions. The algorithms that we present are mainly intended for arbitrary-precision arithmetic. That is, the ...
... addition, multiplication and division, and their connections to topics such as modular arithmetic, greatest common divisors, the Fast Fourier Transform (FFT), and the computation of special functions. The algorithms that we present are mainly intended for arbitrary-precision arithmetic. That is, the ...
Signed integer representation
... Floating-point representation Prepared by Dr. Hassan SALTI - 2012 ...
... Floating-point representation Prepared by Dr. Hassan SALTI - 2012 ...
Significant figures - Acutecaretesting.org
... The uncertainty caused by the rounding to three figures is in the order of ± 0.5 % or less, which in the majority of cases is considered to be acceptable for all analytes and concentration ranges. ...
... The uncertainty caused by the rounding to three figures is in the order of ± 0.5 % or less, which in the majority of cases is considered to be acceptable for all analytes and concentration ranges. ...
JobTestPrep`s Numeracy Review
... Percent means “out of 100”. Percentages are fractions in which the denominator (the bottom part) always has a value of 100. Since the denominator is always the same, it doesn’t need to be written down. That’s why percentages are displayed as just one number instead of two like normal fractions. We t ...
... Percent means “out of 100”. Percentages are fractions in which the denominator (the bottom part) always has a value of 100. Since the denominator is always the same, it doesn’t need to be written down. That’s why percentages are displayed as just one number instead of two like normal fractions. We t ...
CALCULATING TO HUNDREDS OF DIGITS OF ACCURACY by
... Note that this procedure calls multiply 50 times, and hence uses 10,000 integer multiplications, as well as 5000 integer divisions and a comparable number of additions and subtractions. It takes 0.19 seconds for this procedure to be executed on the 16 Mhz IBM 386SX machines in Hanes 02. Generally, t ...
... Note that this procedure calls multiply 50 times, and hence uses 10,000 integer multiplications, as well as 5000 integer divisions and a comparable number of additions and subtractions. It takes 0.19 seconds for this procedure to be executed on the 16 Mhz IBM 386SX machines in Hanes 02. Generally, t ...
Printout 4
... Computer arithmetic is constrained by limited precision Bit patterns have no inherent meaning (side effect of the stored-program concept) but standards do exist two’s complement IEEE 754 floating point Computer instructions determine “meaning” of the bit patterns Performance and accuracy ...
... Computer arithmetic is constrained by limited precision Bit patterns have no inherent meaning (side effect of the stored-program concept) but standards do exist two’s complement IEEE 754 floating point Computer instructions determine “meaning” of the bit patterns Performance and accuracy ...
10 DECIMALS print
... • Rounding decimal numbers is similar to rounding whole numbers: Look at the digit to the right of the given place value to be rounded. If the digit to the right is > 5, then add 1 to the digit in the given place value and zero out all the digits to the right (“hit”). If the digit to the right is ...
... • Rounding decimal numbers is similar to rounding whole numbers: Look at the digit to the right of the given place value to be rounded. If the digit to the right is > 5, then add 1 to the digit in the given place value and zero out all the digits to the right (“hit”). If the digit to the right is ...
10 decimals
... • Rounding decimal numbers is similar to rounding whole numbers: Look at the digit to the right of the given place value to be rounded. If the digit to the right is > 5, then add 1 to the digit in the given place value and zero out all the digits to the right (“hit”). If the digit to the right is ...
... • Rounding decimal numbers is similar to rounding whole numbers: Look at the digit to the right of the given place value to be rounded. If the digit to the right is > 5, then add 1 to the digit in the given place value and zero out all the digits to the right (“hit”). If the digit to the right is ...
10 decimals - Mark`s Academy of Science
... • Rounding decimal numbers is similar to rounding whole numbers: Look at the digit to the right of the given place value to be rounded. If the digit to the right is > 5, then add 1 to the digit in the given place value and zero out all the digits to the right (“hit”). If the digit to the right is ...
... • Rounding decimal numbers is similar to rounding whole numbers: Look at the digit to the right of the given place value to be rounded. If the digit to the right is > 5, then add 1 to the digit in the given place value and zero out all the digits to the right (“hit”). If the digit to the right is ...
Numerical Mathematical Analysis
... 0 ≤ x ≤ M can be stored and represented exactly in floating point form. If n is the number of binary digits in the significand x, all integers less or equal to ...
... 0 ≤ x ≤ M can be stored and represented exactly in floating point form. If n is the number of binary digits in the significand x, all integers less or equal to ...