Notes #4
... * Relatively prime numbers have no common factors other than 1. * A rational number is a number that can be written as a fraction with an integer for its numerator and a nonzero integer for its denominator. ...
... * Relatively prime numbers have no common factors other than 1. * A rational number is a number that can be written as a fraction with an integer for its numerator and a nonzero integer for its denominator. ...
Sums of Continued Fractions to the Nearest Integer
... an integer and two regular continued fractions each of which having partial quotients less than or equal to four. Denoting by F(b) the set of those real numbers x having a regular continued fraction expansion x = [a0 , a1 , a2 , . . . , an , . . .] with arbitrary a0 ∈ Z and partial quotients an ≤ b ...
... an integer and two regular continued fractions each of which having partial quotients less than or equal to four. Denoting by F(b) the set of those real numbers x having a regular continued fraction expansion x = [a0 , a1 , a2 , . . . , an , . . .] with arbitrary a0 ∈ Z and partial quotients an ≤ b ...
Full text in PDF - Annales Univ. Sci. Budapest., Sec. Comp.
... where a0 , a1 are integers and α2 is real (such that the expression on the left makes sense). Hence, the theorem of Cusick & Lee (1.1) immediately implies that every complex number z can be written as the sum of a Gaussian integer and 2b regular continued fractions, where b of them have real partial ...
... where a0 , a1 are integers and α2 is real (such that the expression on the left makes sense). Hence, the theorem of Cusick & Lee (1.1) immediately implies that every complex number z can be written as the sum of a Gaussian integer and 2b regular continued fractions, where b of them have real partial ...
Rounding Rules
... These rightmost digits in exact values are never written down but they are assumed to be there. This is important because in a sense they, too, come from the act of making a measurement, that of counting. In this sense they are significant digits and, therefore, an exact value can be said to have an ...
... These rightmost digits in exact values are never written down but they are assumed to be there. This is important because in a sense they, too, come from the act of making a measurement, that of counting. In this sense they are significant digits and, therefore, an exact value can be said to have an ...
Method 3: Convert Fractions to Decimals
... Solving applied problems is not difficult, but there are multiple methods for doing calculations. I will indicate the 3 methods, and list them in order of preference, according to the most accurate answer achieved. The biggest problem with problems of mixed form is accuracy. Because rounding causes ...
... Solving applied problems is not difficult, but there are multiple methods for doing calculations. I will indicate the 3 methods, and list them in order of preference, according to the most accurate answer achieved. The biggest problem with problems of mixed form is accuracy. Because rounding causes ...
Solutions
... Let x be an arbitrary odd integer and y be an arbitrary integer. By the definition of odd, we know x = 2k + 1 for some corresponding integer k. We will show that if y is odd, xy is odd, and if y is even, xy is even to show both directions of the biconditional. Suppose y is odd. Then by the definitio ...
... Let x be an arbitrary odd integer and y be an arbitrary integer. By the definition of odd, we know x = 2k + 1 for some corresponding integer k. We will show that if y is odd, xy is odd, and if y is even, xy is even to show both directions of the biconditional. Suppose y is odd. Then by the definitio ...
Lesson Overview - Washington Student Math Association
... To round a number to a particular place value, locate the digit to be rounded. Suppose we are to round these numbers to the nearest tenth: ...
... To round a number to a particular place value, locate the digit to be rounded. Suppose we are to round these numbers to the nearest tenth: ...
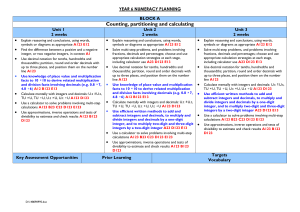
y6 block a plan - School
... subtract integers and decimals, to multiply and divide integers and decimals by a one-digit integer, and to multiply two-digit and three-digit integers by a two-digit integer A23 D123 E13 Use a calculator to solve problems involving multi-step calculations A123 B23 C23 D123 E123 Use approximations, ...
... subtract integers and decimals, to multiply and divide integers and decimals by a one-digit integer, and to multiply two-digit and three-digit integers by a two-digit integer A23 D123 E13 Use a calculator to solve problems involving multi-step calculations A123 B23 C23 D123 E123 Use approximations, ...
Chapter 1 Numerical Algorithms and Roundoff Errors
... Indeed, the error appears to decrease like h. More specifically (and less importantly), using our explicit knowledge of f 00 (x) = − sin(x), in this case we have that 21 f 00 (x0 ) ≈ −0.466. The quantity 0.466h is seen to provide a rather accurate estimate for the above tabulated error values. The a ...
... Indeed, the error appears to decrease like h. More specifically (and less importantly), using our explicit knowledge of f 00 (x) = − sin(x), in this case we have that 21 f 00 (x0 ) ≈ −0.466. The quantity 0.466h is seen to provide a rather accurate estimate for the above tabulated error values. The a ...
Tutorial on the Use of Significant Figures
... significant figures. The three numbers added together should result in a number that is rounded off to the last common significant digit occurring furthest to the right; in this case, the final result should be rounded with 1 digit after the decimal. Thus, the correct rounded final result should be ...
... significant figures. The three numbers added together should result in a number that is rounded off to the last common significant digit occurring furthest to the right; in this case, the final result should be rounded with 1 digit after the decimal. Thus, the correct rounded final result should be ...
Approximate Error
... ➡ For example, an iterative scheme can be developed to obtain the physical quantity G. - If the scheme is well-designed then G(n) approaches the true value of G0 when n→∞. - However, we always have to stop at a finite value of n=N. The truncation error is the difference between G(N) and G(∞). ...
... ➡ For example, an iterative scheme can be developed to obtain the physical quantity G. - If the scheme is well-designed then G(n) approaches the true value of G0 when n→∞. - However, we always have to stop at a finite value of n=N. The truncation error is the difference between G(N) and G(∞). ...
Test - Mu Alpha Theta
... Start with any positive integer (ex. 4,229,301) and count the number of even digits, E, the number of odd digits, O, and their sum, E + O. Create a new number by concatenating the three values (in the order E, O, E+O) into one number and dropping any leading 0’s (for our example it would be 437). Fo ...
... Start with any positive integer (ex. 4,229,301) and count the number of even digits, E, the number of odd digits, O, and their sum, E + O. Create a new number by concatenating the three values (in the order E, O, E+O) into one number and dropping any leading 0’s (for our example it would be 437). Fo ...
2.5 Floating-Point Representation
... we will establish a rule that the first digit of the significand must be 1. This results in a unique pattern for each floating-point number. – In the IEEE-754 standard, this 1 is implied meaning that a 1 is assumed after the binary point. – By using an implied 1, we increase the precision of the rep ...
... we will establish a rule that the first digit of the significand must be 1. This results in a unique pattern for each floating-point number. – In the IEEE-754 standard, this 1 is implied meaning that a 1 is assumed after the binary point. – By using an implied 1, we increase the precision of the rep ...
03-30 7.1 Decimals, 7.2 Adding and Subtracting Decimals
... and Subtracting Decimals To add or subtract decimals: 1) Write the numbers vertically, lining up the decimal points. 2) Place the missing “invisible zeros.” 3) Add or subtract with your favorite old algorithm keeping the decimal throughout. 4) Carry down the decimal point into your final ...
... and Subtracting Decimals To add or subtract decimals: 1) Write the numbers vertically, lining up the decimal points. 2) Place the missing “invisible zeros.” 3) Add or subtract with your favorite old algorithm keeping the decimal throughout. 4) Carry down the decimal point into your final ...
Data Representation
... 2.4 Signed Integer Representation • Although the “end carry around” adds some complexity, one’s complement is simpler to implement than signed magnitude. • But it still has the disadvantage of having two different representations for zero: positive zero and negative zero. • Two’s complement solves ...
... 2.4 Signed Integer Representation • Although the “end carry around” adds some complexity, one’s complement is simpler to implement than signed magnitude. • But it still has the disadvantage of having two different representations for zero: positive zero and negative zero. • Two’s complement solves ...
IOSR Journal of Electronics and Communication Engineering (IOSR-JECE)
... (00=Round to nearest even: This is the standard default rounding. The value is rounded up or down to the nearest infinitely precise result. If the value is exactly halfway between two infinitely precise results, then it should be rounded up to the nearest infinitely precise even. 01=Round-to-Zero: B ...
... (00=Round to nearest even: This is the standard default rounding. The value is rounded up or down to the nearest infinitely precise result. If the value is exactly halfway between two infinitely precise results, then it should be rounded up to the nearest infinitely precise even. 01=Round-to-Zero: B ...
Additional and Subtraction of Integers (PowerPoint)
... Rule: the sum of a positive integer and a negative integer will have the same sign as the integer with the greater absolute value. Step 1: Change the expression to an addition by using the absolute value. Step 2: Plot the first integer on the number line. Step 3: Plot the second integer on the numbe ...
... Rule: the sum of a positive integer and a negative integer will have the same sign as the integer with the greater absolute value. Step 1: Change the expression to an addition by using the absolute value. Step 2: Plot the first integer on the number line. Step 3: Plot the second integer on the numbe ...
Document
... • The largest exponent value (with zero fraction) represents +/- infinity • The largest exponent value (with non-zero fraction) represents NaN (not a number) – for the result of 0/0 or (infinity minus infinity) ...
... • The largest exponent value (with zero fraction) represents +/- infinity • The largest exponent value (with non-zero fraction) represents NaN (not a number) – for the result of 0/0 or (infinity minus infinity) ...
Conversions Among Number Systems
... Floating point numbers are commonly used to approximate the real numbers. It is beyond the scope of this course to provide a complete description of floating point numbers, but some essential ideas should be known before writing solutions to problems that involve real numbers. Floating point notatio ...
... Floating point numbers are commonly used to approximate the real numbers. It is beyond the scope of this course to provide a complete description of floating point numbers, but some essential ideas should be known before writing solutions to problems that involve real numbers. Floating point notatio ...
ppt
... (specified by IEEE Standard 754) is: – 23 bits for the mantissa – 1 bit for the mantissa's sign – 8 bits for the exponent ...
... (specified by IEEE Standard 754) is: – 23 bits for the mantissa – 1 bit for the mantissa's sign – 8 bits for the exponent ...
“1”+ - UNC Computer Science
... – Hint: Zero is small. What’s the smallest number you can generate? – E = Exponent + 127, Exponent = -127, Signficand = 1.0 10 (1.0) x 2-127 = 5.87747 x 10-39 ...
... – Hint: Zero is small. What’s the smallest number you can generate? – E = Exponent + 127, Exponent = -127, Signficand = 1.0 10 (1.0) x 2-127 = 5.87747 x 10-39 ...
REAL NUMBERS CLASS 10 TEST PAPER
... 19. Check whether 5 × 7 × 11 + 6 is a composite number. 20. Check whether 7 × 6 × 3 × 5 + 5 is a composite number. 21. Express 143 as product of its prime factors. 22. Find LCM and HCF of 120, 250 and 355 by the prime factorization method. 23. Find the LCM and HCF of 16 and 240 by the prime factoriz ...
... 19. Check whether 5 × 7 × 11 + 6 is a composite number. 20. Check whether 7 × 6 × 3 × 5 + 5 is a composite number. 21. Express 143 as product of its prime factors. 22. Find LCM and HCF of 120, 250 and 355 by the prime factorization method. 23. Find the LCM and HCF of 16 and 240 by the prime factoriz ...
PowerPoint
... • The answer, when you add or subtract, can not be better than your worst estimate. • You have to round the answer to the place value of the measurement (in the problem) with the greatest uncertainty. ...
... • The answer, when you add or subtract, can not be better than your worst estimate. • You have to round the answer to the place value of the measurement (in the problem) with the greatest uncertainty. ...
IOSR Journal of Electronics and Communication Engineering (IOSR-JECE)
... The five possible exceptions are: 2.6.1) Invalid: Operation are like square root of a negative number, returning of NaN by default, etc., output of which does not exist. 2.6.2) Division by zero: It is an operation on a finite operand which gives an exact infinite result for e.g., 1/0 or log (0) that ...
... The five possible exceptions are: 2.6.1) Invalid: Operation are like square root of a negative number, returning of NaN by default, etc., output of which does not exist. 2.6.2) Division by zero: It is an operation on a finite operand which gives an exact infinite result for e.g., 1/0 or log (0) that ...