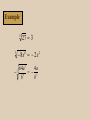* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download mginter4e_ppt_7_1
Survey
Document related concepts
Transcript
Intermediate Algebra Chapter 7 Section 7.1 • Opposite of squaring a number is taking the • • square root of a number. A number b is a square root of a number a if b2 = a. In order to find a square root of a, you need a # that, when squared, equals a. The principal (nonnegative) square root is noted as a The negative square root is noted as a • Radical expression is an expression • • containing a radical sign. Radicand is the expression under a radical sign. Note that if the radicand of a square root is a negative number, the radical is NOT a real number. Example 49 7 5 25 16 4 4 2 • Square roots of perfect square radicands • • simplify to rational numbers (numbers that can be written as a quotient of integers). Square roots of numbers that are not perfect squares (like 7, 10, etc.) are irrational numbers. IF REQUESTED, you can find a decimal approximation for these irrational numbers. • Otherwise, leave them in radical form. Do not convert to an approximation unless requested to do so. Radicands might also contain variables and powers of variables. Example Simplify. Assume that all variables represent positive numbers. 64x10 8x 5 2 20 25a b 5ab 10 The cube root of a real number a 3 a b only if b 3 a Note: a is not restricted to non-negative numbers for cubes. The cube root of a negative number is a negative number. Example 3 3 27 3 8x 2x 6 3 4 a 64 a 3 3 9 b b 2 Other roots can be found, as well. The nth root of a is defined as n a b only if b n a If the index, n, is even, the root is NOT a real number when a is negative. If the index is odd, the root will be a real number when a is negative. Example Simplify the following. Assume that all variables represent positive numbers. 4 2 2x 16x 8 2a 32a 2a 15 3 3 b b b 5 5 n If the index of the root a is even, then the notation represents a positive number. But we may not know whether the variable a is a positive or negative value. Since the positive square root must indeed be positive, we might have to use absolute value signs to guarantee the answer is positive. If n is an even positive integer, then n an a If n is an odd positive integer, then n a a n Example Simplify the following. 2 20 25a b 5ab 10 5 a b10 If we know for sure that the variables represent positive numbers, we can write our result without the absolute value sign. 2 20 25a b 5ab 10 Example Simplify the following. 3 4 a 64 a 3 3 9 b b Since the index is odd, we don’t have to force the negative root to be a negative number. If a or b is negative (and thus changes the sign of the answer), that’s okay. Since every value of x that is substituted into the equation yn x produces a unique value of y, the root relation actually represents a function. The domain of the root function when the index is even, is all nonnegative numbers. The domain of the root function when the index is odd, is the set of all real numbers. We have previously worked with graphing basic forms of functions so that you have some familiarity with their general shape. You should have a basic familiarity with root functions, as well. Example x y 6 6 4 2 2 1 2 1 0 0 Graph y x y (6, 6 ) (4, 2) (2, 2 ) (1, 1) x (0, 0) Example x y 8 2 4 3 y 4 1 1 0 0 -1 -1 -4 4 -2 -8 Graph y 3 x 3 3 (4, 4 ) (8, 2) (1, 1) (-1, -1) (-8, -2) (-4, 3 4) (0, 0) x