Download Basic Characteristics of Electromagnetic Radiation.

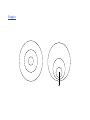
Basic Characteristics of Electromagnetic Radiation.
Brief review of EM waves, with a view towards astronomical application.
I. Traveling wave characteristics
E&M radiation consists of transverse waves
with alternating electric and magnetic fields,
and amplitudes given by:
r r
 2π

E = E o sin
( x − ct )
 λ

where: Eo is the electric amplitude, λ is the
wavelength, and c is the propagation speed.
The wavelength and frequency are related by the
Dispersion relation:
λν = c, in vacuo.
From notes for MIT Physics 8.02,
Electricity and Magnetism
Wavelengths and frequencies: the EM spectrum
From Wikipedia: electromagnetic spectrum
Atmospheric transmission.
From NASA Goddard Space Flight Center
Important wave-like properties:
Diffraction:
Waves bend around obstacles.
Every unobstructed point on a wavefront will act a source of
secondary spherical waves. The new wavefront is the surface
tangent to all the secondary spherical waves.
From notes for MIT Physics 8.02, Electricity and Magnetism
Interference:
e.g., double-slit (Young’s) pattern of interfering waves.
The amplitudes of the overlapping waves add directly, but the brightness or intensity
depends on the square of the sum (where a 1-d. equation is used for simplicity).

 2π

 2π

I ∝  E 1 sin 
( x1 − ct ) + E 2 sin 
(x 2 − ct )  
 λ

 λ


2
II. Light Rays, Geometric Optics.
is often a convenient way to look at EM wave propagation. The ‘rays’ are
straight normals to local wave fronts, with the following properties.
Reflection: Equal angles of incidence and reflection as measured from a normal to the
surface. This principle allows mirrors to focus light.
Refraction (dispersion): Generally light rays are bent as they pass through the
boundary between two media, or through a medium with a temperature or pressure
gradient. Dispersion results whern the bending (or index of refraction) depends on
wavelength.
Ray optics + Huygens’ wave principle help us better understand diffraction and
interference.
2 slits again Δx = λ
Δx = λ/2
Δx = 0
Intensity
Mirror reflection:
Width of central
diffraction peak:
θ ≈ λ/d,
where d is the
aperature size. This
gives,
Δx = 0
Δx = λ
θ = 5 x 10-7 rad =
0.1 arcsecond for a
1 m diameter
telescope.
Reverse diffraction pattern
III. Particle Aspect of Electromagnetic Radiation.
In addition to its wave nature, electromagnetic radiation also seems to come
in discrete bundles of energy called ‘photons.’ The energy of a photon
depends on the frequency of the radiation via Planck’s law:
ε = hν = hc/λ.
This relation connects the wave-particle dual characteristics of EM radiation.
The particle aspect is most relevant at high energies, or very low light levels,
i.e., where there are few photons.
The Doppler Effect
Often explained by analogy to sound or water waves. See squeezed wave
diagram below.
Full special relativistic expression for wavelength of light from a moving source
is,
1/ 2
λ 1+ v /c 
=
.

λo 1− v /c 
When v/c << 1, we can approximate this by,
€
λ / λo ≈ (1+ 12 vc )(1− (− 12 vc )) ≈ 1+ v /c,
Δλ λ − λo λ
so,
=
=
−1 ≈ v /c.
λo
λo
λo
€
Doppler
Intensity and Flux
To describe the flow (and scattering) of radiation we need the definitions of
intensity and flux, which quantify the idea of a directed, density of radiation.
Monochromatic intensity - is the amount of energy in the frequency interval (ν,
ν+Δν) flowing through a unit area, per unit time, into a cone of unit solid angle,
in a given direction.
r
Iν =
€
ΔE
nˆ
Δν ΔAΔtΔΩ
J
.
2
s ⋅ m ⋅ Hz ⋅ ster
ΔΩ
Monochromatic flux - is easier to define! Integrate intensity in solid angle over
a hemisphere. Thus, flux is the energy in frequency range (ν, ν+Δν) flowing
through a unit area per unit time, and into ‘any’ direction (of the hemisphere).
ΔA
__________________________________
Alternately, the flux received at a detector is the total incoming energy per
unit time, etc., from any angle (though often from a single point source).