Download Algebra 1 Lesson 1

8/20/16
Algebra 1
Lesson 1-3
Common Core
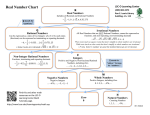
Real Numbers and the Number Line
Real Numbers
Rational Numbers
Integers
Whole Numbers
Irrational
Numbers
Natural Numbers
1
8/20/16
Natural Numbers
• what you see in nature
• counting numbers
• positive numbers
– any number greater than zero
– always to the right of zero
0
2
8/20/16
Whole Numbers
• includes all natural numbers
• zero
1 2 3 4 5 6
Integers
• Includes all whole numbers (0, 1, 2, 3, …)
• Negative numbers (opposites of whole
numbers)
– any number less than zero
– always left of zero
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6
3
8/20/16
Terminating Decimals
• A number written as a decimal where the
number has a limited number of digits. (It
has an ending)
• What are examples?
Repeating Decimals
• A number written as a decimal where there
is a repeating pattern of digits that NEVER
ends.
• What are examples?
4
8/20/16
Rational Numbers
• All integers
• Decimals that have an ending (terminate)
OR repeat indefinitely
0.5
0.25
-0.333…
1.272727…
• Fractions, a/b where a and b are integers
and b ≠ 0.
Examples:
1
2
-2
3
17
5
3
1
5
8/20/16
6
8/20/16
Irrational Numbers
• Cannot be written as a
fraction (ratio of 2 intergers)
• Decimal goes on forever
without repeating (never ends)
Example: Pi
3.1415926535897932384626433832795…
You can classify numbers using sets…
• Set: a well-defined collect of terms
– Example: The set of all integers
{…-3, -2, -1, 0, 1, 2, 3…}
• Element of the Set: members of a set
– Example: What are 3 elements of the above set?
-1, 1, 100
• Subset: elements from a given set
– Example: What are the natural numbers with the
above set of integers?
{1, 2, 3…}
7
8/20/16
Real Numbers
Rational Numbers –
fractions & terminating or
repeating decimals
Integers
(… -3, -2, -1, 0, 1, 2, 3…)
Whole Numbers
(0, 1, 2, 3…)
Irrational
Numbersdecimals that
go on forever
that DO NOT
repeat
Natural Numbers
(1, 2, 3…)
I’d Rather Be…
Rational verses Irrational
If you could be a number, would you rather be
rational or irrational? Write your response on
a sticky note, explain why and then post it on
the whiteboard.
8
8/20/16
Classify each number:
Classify each number
✔
✔
✔
✔
✔
✔
✔
✔
✔
✔
✔
✔
✔
✔
✔
9
8/20/16
Square Roots
• An operation that yields a number which, when
multiplied by itself produces the given number
• Example:
16
Radical
sign
Parts of a Radical
10
8/20/16
Inverse Operations
(Opposite Operations)
What is the opposite of…
Subtraction
Addition
Division
Multiplication
Squaring a Number
Square Root
Square Roots
• If a ³0 and a2 = b, then a is the square root of b.
Squares
Square Roots
0= 0
02 = 0
12 = 1
1= 1
22 = 4
4= 2
2
3 =9
9= 3
42 =16
What is the
16
= 4
relationship
between Squares
and Square
Roots?
11
8/20/16
Inverse Operations
(Opposite Operations)
What is the opposite of…
Subtraction
Addition
Multiplication
Squaring a Number
Division
Square Root
Square Roots
• If a ³0 and a2 = b, then a is the square root of b.
Squares
Square Roots
0= 0
02 = 0
12 = 1
1= 1
22 = 4
4= 2
Perfect Squares2
3square
= 9 roots that are
9= 3
whole
16 numbers
42 =
(There are 11 of them
16
= 4
from 0 to 100. Can
you name them?)
12
8/20/16
Perfect Square
Roots: square
If a perfect square
root gives
a
roots that have
ayou
whole
number
whole answer…What
as anifanswer
happens
it is NOT
0= 0
a perfect square?
25 = 5
It is an irrational
number
1=
1
4=
2
49 = 7
9=
3
64 = 8
16 = 4
81 = 9
100 = 10
36 = 6
BrainPop Video & Do It Review
Square Roots & Perfect Square Roots
• http://www.brainpop.com/math/numbersando
perations/squareroots/
13
8/20/16
Try This…
• Use a calculator to approximate the 3
• Write the number on a piece of paper
• Enter it into your calculator, square it, then
subtract 3.
• Do you get 0?
• EXPLAIN
Watch this video…
…you never know when you may lose out on
money because you do not know about square
roots!
• http://www.youtube.com/watch?v=BbX44Y
SsQ2I
14
8/20/16
Non-Perfect Square Roots
Use estimation to figure out the square root of 14…
14 is between what
2 perfect squares ?
9 = 3
9 &
16
16 = 4
Therefore the square root of 14 is a irrational
number between 3 & 4. Check your calculator
to see the exact irrational number.
15
8/20/16
√25 & √36 √81 & √100
5&6
9 & 10
≅6
≅9
-√4 & -√9
-2 & -3
≅ -3
Another way to approximate
square roots…
Watch this video ….
https://docs.google.com/file/d/0BV_py0ic4ugNlplcXRtdjJtc1k/edit?pli=1
16
8/20/16
Try these in your
calculator:
25 = 5
5
5
144 = 12
12
12
23,104 = 152
152
152
17
8/20/16
Look at these
examples again…
25 = 5
5
25 = 5
OR
5
-5
-5
What is a negative number multiplied by
another negative number?
A positive
So…how many answers are there to every square root problem?
Why?
Find the Square Root and then
determine if it is rational or
irrational
196
14
121
50
4
16
2
3
18
8/20/16
Non-Real Numbers
−4
−16
What is
difference
about these
examples?
−25
−36
−100
Look at these
examples again…
25 = 5
5
5
25 = 5
OR
-5
-5
What is a negative number multiplied by
another negative number?
A positive
Therefore, you will always have a positive number
under your radical sign.
19
8/20/16
3 Kinds
of Square Roots
When you first learned
about
square roots. You
Principal Square
Root
only learned about principle
-all #s are positive
square roots. Now that you
know your Integer Rules
Negative Square
Root
and
more about square
-negative signroots…you
appears know that ALL
outside the radical
signroots have 2
square
64 = 8
− 64= −8
answers!
Both Square Roots
-both the negative &
positive signs are used
± 64 = ±8
3 Kinds of Square Roots
Principal Square Root:
The number that is multiplied by itself is a
positive number
Example:
64 = 8
You typically do not add the
positive sign in front of the
problem and answer. The
positive is implied!
20
8/20/16
3 Kinds of Square Roots
Negative Square Root:
The number that is multiplied by itself is a
negative number (Remember: a negative
times a negative is a positive)
Example:
− 64= −8
The negative sign appears outside
the radical sign. So your answer
must have a negative sign too!
3 Kinds of Square Roots
Both Square Roots:
The number that is multiplied by itself could
be BOTH a negative & positive
number
Example:
± 64 = ±8
The negative sign and positive signs
appear outside the radical sign.
So your answer must have
BOTH signs!
21
8/20/16
Find each square root.
If necessary, round to the nearest hundredth.
1.
49
2.
− 78
7
-8.83
€ 3. ± 513
€
€
4.
±22.65
1
2
25
100
€
Cube Roots
• An operation that yields a number which, when
multiplied by itself three times produces the
given number
Example:
3
8= 2
What multiplied by itself
three times equals 8?
Radical sign
3
22
8/20/16
Perfect Cube Roots: cube roots
that have a whole number as an
answer
3
3
0 = 0
1= 1
3
3
125 = 5
1000 = 10
216 = 6
8= 2
3
343 = 7
3
27 = 3
3
512 = 8
3
64 = 4
3
729 = 9
3
3
E
C
A
D
F
B
23
8/20/16
What are the symbols of
inequality?
24
8/20/16
Write >, <, or = to make the sentence true.
1.
2.
€
€
€
3.€
5.72
1
7
2
9
> 5
1
< 7
= 0.2
€
25
8/20/16
Write each set of numbers in order from least
to greatest.
1.
0.42, 0.63,
0.63,
€
0.42,
4
3
4
3 €
2.
8, − 4.83, 0.4
−4.83, 0.4,
8
The Code Name Organizer
Students will need:
• Name Decoder Chart
• Poster Board
• Markers
26
8/20/16
27