Download Electric Potential - McMaster Physics and Astronomy

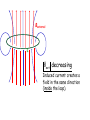
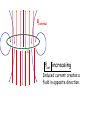
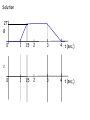
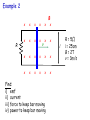
Magnetic Induction
- magnetic flux
- induced emf
- Faraday’s Law and Lenz’s Law
Magnetic Flux
Flux through a surface S:
 B   B  dA
S
(dA is the “area vector”, perpendicular to the surface.)
- a scalar ; units, 1 T·m2 = 1 Weber (Wb)
- represents “number of magnetic field lines
through a surface S”
Magnetic Flux
Flux through a closed
surface S:
 B  dA  0
S
This is like Gauss’ law, but for magnetism. However, it
states that:
- the number of magnetic field lines that enter a
volume enclosed by a surface S must equal the
number that leave the volume
- and it implies that magnetic monopoles do not exist
Faraday’s Law:
When the external magnetic flux ΦB through a
closed conducting loop with one turn changes, the
emf induced in the closed loop is:

d B

dt
(for a loop with N turns:
Note that ΦB changes if:

d B
)
 N
dt
   dtd BA cos  
1) B changes
2) the area of the circuit changes (dA)
3) the orientation of the circuit changes (B•dA)
Lenz’s Law (the negative sign)
(for the direction of the induced emf)
The induced emf and induced current
direction in the loop is such that the
magnetic flux it produces inside the loop
opposes the change in flux inside the loop
produced by the external field.
The induced emf is directly proportional to
the rate of change of the magnetic flux
thought the circuit.
The “-” sign:
Field vector B
positive current
direction
For given B direction the R.H. rule defines a
corresponding “positive” current and emf direction.
e.g.
B , increasing:
B , decreasing:
ε
induced ε
induced
is –ve
is +ve
Induction
Move a magnet at constant speed through a coil
attached to a voltmeter:
B
v
S
N

S
N
+ve current direction
voltmeter
reading

position
x
Bexternal
ε

Bext decreasing
Induced current creates a
field in the same direction
(inside the loop).
Bexternal
ε

Bext increasing
Induced current creates a
field in opposite direction.
Example 1
Circular coil, 100 turns, area = πr2 = 0.10m2
x x x x

B is an external magnetic
field, and is changing with
time as in the graph below.
x x x x
x x x x
x x x x
2T
B
0
1
1.5
2
3
4 t (sec.)
Plot emf, paying attention to its sign.
Note: CW is the direction of positive emf
Solution
2T
B
0
1
1.5
2
3
4 t (sec.)
0
1
1.5
2
3
4 t (sec.)
ε
Quiz
A circuit of area A is made from a single loop of
wire connected to a resistor of resistance R. It is
placed in a uniform external field B (at right
angles to the plane of the loop). B is reduced
uniformly to zero in time Dt. The total charge
which flows through the resistor is:
A)
B)
C)
D)
independent of Dt
proportional to Dt
inversely proportional to
zero
Dt
Motional emf
• emf induced in a conductor moving through
a magnetic field.
Conductor moving in uniform B :
Force on charge q:

x
x
x
x
x
x
x
x
x
E
x
x
Fm
x
x
x
+
x
B
Fm  qvB
As the positive charge moves slowly
along the conductor, parallel to Fm ,
the work done on each charge is:
x
x
W = Fm l = qBvl
The emf (work per unit charge)
induced between the bar ends is:
x
ε = W/q
x
x
v
  Bvl
Which end of the rod is positive after some time?
What is the “E ” for?
x
x
x
x
x
x
x
x
x
x
x
x
x
l
v
x
x
x
x
x
x
x
x
x
x
x
x
B
We can derive the same
expression, ε = Bvl, from
Faraday’s Law, if we look
at a simple complete
circuit. Consider a
conducting bar sliding
along a a U-shaped
conductor as shown.
Area enclosed by closed loop = A = l x
d
d
dx
 
  ( Blx)   Bl   Bvl
dt
dt
dt
What is the direction of the induced current?
Example 2
R
x
x
x
x
x
x
x
x
x
x
v
B
x
x
l
x
x
x
x
x
x
x
x
x
x
x
x
Find:
i) emf
ii) current
iii) force to keep bar moving
iv) power to keep bar moving
R = 5Ω
l = 25cm
B = 2T
v = 3m/s
Solution
Example 3
A bar of mass m and length l moves on two frictionless
parallel rails in the presence of a uniform B directed
into the paper. The bar is given an initial velocity vo to
the right and is released.
Find the:
a) velocity of the bar as a function of time
b) induced current
B
c) induced emf
x
x
R
x
x
vo
x
x
l x
x
x
Solution
Summary
Faraday’s Law:
A changing magnetic flux induces an emf in a circuit:

d B

dt
Lenz’s Law: (for direction of ε)
The induced emf causes an induced current whose
flux would oppose the change in external flux
through the loop.