Download Conductive heat flow at the surface is described by Fourier`s law of

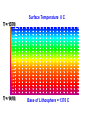
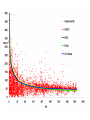
Will Gosnold
Heat Flow in Young Oceanic Crust:
Is Earth’s Heat Flux 44 TW or 31 TW
2008 Joint Assembly, Ft. Lauderdale
T21A-01, May 27, 2008
T-21A Thermotectonic Models of the Oceanic Lithosphere and the
Problem of Hydrothermal Circulation: A New Look
Outline
•
•
•
•
•
•
Statement of problem
Heat flow data
Continental and marine heat flow
Heat flow vs. age models
2-D numerical models
Sumary and conclusions
20,201 heat flow sites recognized by the International Heat Flow Commission
At issue is the
accuracy of models of
heat flow vs. age.
q = 510 t -.5
q = 480 t -.5
q = 473 t -.5
Surface Heat Flow
q  
Conductive heat flow at the
surface is described by
Fourier’s law of Heat
conduction
n
Assuming we know heat flow,
temperature at depth “z” may
be calculated by
Tz  
i 1
qzi
i
Conductive heat flow
is predictable
Continental heat flow
decreases with
depth
Sources are heat
contained with the
crust and mantle and
radioactive heat
production
In a conductive environment
with constant heat flow, the
temperature gradient varies
with thermal conductivity.
q  
A fundamental
assumption is
that the
temperature
gradient is
vertical and
heat flow
calculated from
the gradient is
vertical heat
flow.
Topography and
complex structure
with thermal
conductivity
contrasts or
transient sources
and sinks such as
water flow
invalidate this
assumption.
Heat flow in conductive
environments is
predictable and the heat
flow map of North
America demonstrates
this predictability on the
continents and in the
ocean basins.
High heat flow:
young crust and recent
tectonics
Low heat flow:
old thermally stable
crust
Variation in conductive
heat flow within heat flow
provinces on the
continents is due to
variation in radioactive
heat production.
q = q0+ AD
Heat flow within ocean basins correlates with age.
Continental heat flow exhibits low variability
in non-tectonic areas.
Variability of q vs distance east
of the Rocky Mts.
Marine heat flow exhibits high variability everywhere.
Variability of q vs distance from ridge
Bullard’s
Law and continental
Side-by-side comparison
of marine
heat flow
presence
of non-conductive
"Never
takesuggests
a secondthe
heat
flow measurement
within 20
and
transient
signals
marine
km of
the original
for in
fear
that itenvironments
differ from theand
firstinby
young tectonictwo
environments.
orders of magnitude."
2-D finite-difference heat flow model
• Temperature profile for the ridge crest and
intraplate from D.H. Green
• Temperature at base of intraplate lithosphere
1370 C
• Thermal conductivity profile from Hofmeister
(1999) and van den Berg, Yuen, and Steinbach
(2001)
• Half-spreading velocities of 1, 2.5, 5,&10 cm y-1
Surface Temperature 0 C
T = 1370
T = 1410
Base of Lithosphere = 1370 C
Thermal Conductivity: Hofmeister (1999); van den Berg, Yuen, Steinbach (2001)

3
K0 P
298 a
k (T , P)  k 0 (
) exp[ 4  1 / 3) (T  298)](1 
)   bi T i
T
K0
i 0
k0 = 4.7 WK-1m-1
T in deg K, P in Pa
Gruenheissen Paramteter, γ = 1.2
Thermal expansion coefficient, α = 2.0 x 10-5 K-1
Bulk modulus, K0 = 261 GPa
Pressure derivative of the bulk modulus, K0' = 5
The fitting parameter, a = 0.3
Each node in the
model exchanges
heat with its eight
nearest neighbors in
two processes:
conduction and
advection. Iteration
time for each
calculation is
controlled to maintain
stability in the model.
Surface Temperature 0 C
T = 1370
T = 1410
Base of Lithosphere = 1370 C
Temperature and heat flow gradient from
ridge crest to 19 Ma (474 km @ 2.5 cm y-1)
0
1400
1300
-20,000
1200
1100
1000
Depth (m)
-40,000
900
800
-60,000
700
600
-80,000
500
400
-100,000
300
200
100
-120,000
0
40000
80000
120000
Age (y/100)
160000
0
HF at 0 Ma = 1577 mW m-2
HF at 0 Ma =
∞
HF at 0 Ma =
∞
HF at 0 Ma =
∞
Summary and conclusions
• Conductive heat flow is predictable.
• Side-by-side comparison of marine and
continental heat flow suggests extreme nonconductive and transient signals in marine
environments and in young tectonic
environments.
• To test analytical models of heat flow at ocean
ridges, we created a 2-D finite-difference model
of lithosphere spreading.
Summary and conclusions
• The output of the model is a 2-D temperature-depth grid
that provides a comparison with various analytical
models of oceanic heat flow.
• We tested the reliability of the computations using
different half-spreading rates and different node
spacings and verified that the models yield equivalent
results at equivalent times and depths.
• Our results show that the GDH1, HSC, and PSM models
overestimate heat flow close to the ridge, but the
differences are small.
• Our model does not provide evidence that heat flow is
less than 44 TW.
0
1400
1300
-20,000
1200
1100
1000
Depth (m)
-40,000
900
800
-60,000
700
600
-80,000
500
400
-100,000
300
200
100
-120,000
0
40000
80000
120000
Age (y/100)
160000
0
• Heat is transported laterally by advection.
Plates move at different rates at different times
and heat flow is higher farther out in fast moving
plates.
• After 10 MA of not moving, the 12 km thick
lithosphere lost all of its heat for advection.
• Do separate segments of the plates move at
different rates?
• It is the difference in velocity at the ridge that
matters because there is no other source of
heat.