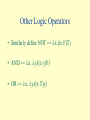Download Lambda Calculus and Lisp

Lambda Calculus and Lisp
PZ03J
Lambda Calculus
• The lambda calculus is a model for
functional programming like Turing
machines are models for imperative
programming. The basic lambda calculus
has just 3 constructs: variables, function
definition (creation), and function
application.
Grammar
• The terminals are variables x, y, z, … and also
lambda, period, parentheses and numbers.
• M -> x | (M M) | x.M
• If F and A are both  expressions then so is (F A)
and indicates the application of the function F with
A as its parameter.
• If F is a  expression then so is x.F This is a
function definition and is also called an
ABSTRACTION because it generalizes the
expression F for any value substituted for x.
Example of Function Definition
• x.x is a way of expressing the identity
function f(x) = x without having to give it a
name.
• x.2x represents the function f(x) = 2x
Bound and Free Variables
• A bound variable is a variable that is in the scope
of a declaration (lambda binding) for that variable.
A variable that is not bound is free. In the
expression:
x. y.(x z)
x is bound and z is free (the y-binding has no
effect as there is no y in the body of the
expression)
• Examples: x. y.(yz)
x.(x b)
Bound Variables
• Any bound variable may have its name
changed without altering the meaning of the
 expression. Just change all occurrences
of the variable in that scope.
• x.x is the same as y.y
• However, x. x.x is the same as x. y.y
(scope rules)
Scope of Lambda Bindings
• In the expression x.F, the scope of the
declaration (or lambda binding) x is
limited to F.
x y x x yx x)
• Frequently the parentheses are left off when
it will not cause confusion.
• In these cases, remember:
– Application is left associative:
a b c = ((a b) c).
– There is only one lambda expression in the
body of an abstraction. (x.x y)
Reduction
• The Reduction Operation (also called
application or evaluation)
• In (F A), the function F is applied with the
parameter A.
• (x.x b) => b
• (x.xy b) => by
Constants and functions
• We can add constants (both for variables
and functions), like 0, 1, 2 …, plus
(x.x 4) => 4
(plus 5 4) => 9
• Here “plus” stands for x.(y.x+y)
• There is sometimes a choice of order of reduction.
When the reduction of a lambda expression
terminates (it doesn't always), the order of
evaluation makes no difference.
Evaluate:
(x.(xxx) (x.x a))
one way => (x.(xxx) (a)) => (aaa)
other way => (x.x a) (x.x a) (x.x a) => aaa
• Some expressions do not terminate
(x.(xx)) (x.(xx))
• and some get more complicated (can you
find an example??
Modeling Logic
• Lambda expressions can be used to model
arithmetic (plus 4 5)
• How can we define lambda expression to give us
arithmetic and logic? Define TRUE and FALSE so
that we can use them in an conditional statement
A B C
where if A reduces to True then the result is B, if A
reduces to False then the result is C (like C
expression z = (a>b)? a: b; //z gets max(a,b)
Defining True and False
• Define T == x. y. x and F == x. y. y
• T P Q => (x. y. x) P Q => (y.P) Q => P
• F P Q => (x. y. y) P Q => (y.y) Q => Q
Other Logic Operators
• Similarly define NOT == x.((x F)T)
• AND == x. y.((x y)F)
• OR == x. y.((x T)y)
Lambda Calculus Models
Functional Programming
Languages
• Imperative languages are abstractions of the
Von Neumann architecture; a computation
is done by performing a sequence of
operations that changes the values of
memory locations through assignments.
• Functional languages do computations by
defining functions and evaluating
expressions.
Style Comparison
• Imperative: sequence, iteration, conditional
• Functional: functional composition, recursion, conditional
• Imperative: change the value of existing object with
assignment
• Functional: compute a new object (garbage collection issues)
• Imperative: side-effects can cause errors
• Functional: no side effects (or limited to I/O) leads to
referential transparency – if you call a function with the
same parameters, you always get the same result.
Structure of Functional Programs
• Functional languages (FLs) have primitive
functions and a mechanism for defining new
functions and an expression evaluator that
will evaluate an expression using the
primitive and newly defined functions.
• A functional program usually consists of a
series of function definitions followed by an
expression using those functions.
Functional Composition
• FLs rely on functional composition instead
of sequence.
f(x) = x + 1
g(x) = x * 2
• Instead of (imperative style)
x = x + 1;
x = x * 2;
• we say g(f(x))
First Class Values
• Functions as first class values: functions can
be passed as parameters and returned.
• A function that returns a function as its
result is a "higher order" function.
Lisp and Scheme
• Lisp was the first FL and is the one most people
think of. It has a simple syntax using prefix
notation and parentheses.
• Scheme is a dialect of Lisp. It has static scope
rather than dynamic, uses meaningful identifiers,
true and false are #T and #F, predicates end in ?
( so (atom? (x) ) returns #F because x is not an
atom (it is a list). Also uses prefix notation.
Lists: the Built-in Data Structure
• Lists consist of elements (atoms (symbolic
and numeric) and lists) separated by spaces
and enclosed in parentheses. The basis data
structure is a 'cons' cell.
• Ex. three lists each with 3 elements
(ALPHA BETA GAMMA)
(12 14 16)
( (A B) (HELLO THERE) 94)
Internal Representation
(ALPHA BETA GAMMA)
(12
ALPHA
14 16)
12
BETA
GAMMA
14
nil
16
nil
Representation of Lists
( (A B) (HELLO THERE) 94)
A
B
94
nil
HELLO
THERE
nil
nil
Exercises
• Diagram :
( (0 2) (1 5) (2 3) )
• Identify the following as atoms, lists, or neither. If
a list, how many elements are in the (top level) list?
ATOM
(this is an atom)
( ( (3) ) )
( ( )
((a b) 3 (c d e))
(* (+ 3 1) (+ 2 1) )
Working with Lists
First and Rest takes lists apart (CAR and CDR,
Head and Tail)
First (12 14 16) is 12
Rest (12 14 16) is (14 16)
First ( Rest (12 14 16) ) is?
NOTE: Rest always returns a list! The empty list is
written () or nil. So, rest of (12) is (). First
and rest only work on lists
Set and Quote
set listA = ' ( (A B) (HELLO THERE) 94)
Note, set makes listA into a constant. It is
"assigned" this string literal, but it cannot be
changed. Also, the single quote means to take what
follows as a literal and not try to evaluate it. What
do the following expressions evaluate to?
rest (first listA)
first (first (rest listA ) )
Making Lists with CONS
CONS takes an expression (atom or list) and a list, puts them
together and returns a new list whose first element is the
expression and remaining elements are those of the old list.
cons a '(b c)
constructs the list (a b c)
(cons (first listA) (rest listA) ) puts together a list just like listA
(first (cons a x) ) = a
(rest (cons a x) ) = x
Doing Arithmetic
The operators + - * / do what you think they would:
(+ 3 4)
evaluates to
7
(- 3 1)
evaluates to
2
(/ 3 1)
evaluates to
3
(- 24 (* 4 3))
evaluates to
12
Note: on most systems, (/ 1 3) will evaluate to 1/3.
Equality operators: = works on numeric symbols and numbers;
EQUAL? works on any atom; equality for lists?
Defining Functions
(DEFINE (name para) (body) )
Examples:
(DEFINE (square a) (* a a) )
(DEFINE (second list) (First (Rest list)))
Conditionals
(IF (condition) (then_part) (else_part) )
(COND (p_1 expression-or-expr-list)
(p_2 expression-or-expr-list)
…
(p_n expr)
(ELSE expr)
;; ELSE is #T
)
;; exp associated with first true p_x is executed
Example: Fibonacci Numbers
F(0) = 1, F(1) = 1, F(n) = F(n-1) + F(n-2)
Number sequence is: 1 1 2 3 5 8 13 21 …
(define (fib n)
(if (or (= n 0) (= n 1) )
1
(+ (fib (- n 1) )
(fib (- n 2) )
)
)
)
Higher Order Functions: map
The function map takes a function and a list as
parameters and returns a list with the function applied
to each element of the original list.
(define map (f x)
(cond ( (nil x) nil )
(else (cons (f (first x))
(map(f (rest x)) ) ) )
)
)
Example with map
(define TimesTen
(* 10 x)
)
Then (map TimesTen
returns the list ??
x
'(12 14 16) )
CAR and CDR
CAR and CDR instead of FIRST and REST:
Both LISP and Scheme allow the CAR and
CDR functions to be combined in a
composite form. That is, assuming x is a
list,
(CAR ( CDR x) )
can be written (CADR x)
More CAR and CDR
The general form is: CxxxR where you can have
any number of x's (at least one) and each x is A or
D signifying CAR or CDR. The order of the A's
and D's indicates the order of CAR's and CDR's in
the expression. Thus,
(CDAR x)  (CDR( CAR x))
(CADDR x)  (CAR( CDR( CDR x)) )
What is (CADADR '( (a b) (c d) (e f) ) )
Predicates in Scheme
•
•
•
•
NULL?
EQ?
LIST?
ZERO?
is this an empty list?
are two atoms equal?
is parameter a list?
is a numeric zero?
Equality for Simple Lists
(DEFINE (eqsimple L1 L2)
(COND
((NULL? L1) (NULL? L2))
((NULL? L2) ‘() )
((EQ? (CAR L1) (CAR L2))
(eqsimple (CDR L1) (CDR L2) ) )
(ELSE ‘() ) ) )
Lambda Calculus and Lisp PZ03J
• Coen256/NotesCh4.doc
• Coen171/FunctionalProgramming.doc