Download UNIFORM RANDOM NUMBER GENERATION Chapter 7 (first half)

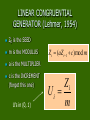
UNIFORM RANDOM NUMBER
GENERATION

The goal is to generate a sequence of

Uniformly distributed

Independent

X1, X2, …. IID Unif[0, 1]
These are the basis of generating all random variates in
simulations
UNIFORM [0,1]
f(x)
Every real number beteween
0 and 1 is equally likely…
1
x
0
1
EARLY METHODS USED PHYSICAL
PHENOMENON

Spinning disks with digits on them

Dice (generate on 1/6, 2/6, …, 1)

Picking people out of the phone book


Picking the nth (n = 1200, 1201, …) digit
in p
Gamma ray photon counting
SEQUENCIAL COMPUTER-BASED
METHODS


Antique Mid-Square Method (Von Neumann)

Z0 is a four-digit number

Z1 = middle four digits of Z02

Z2 = middle four digits of Z1
Ui = Zi/10000
SAMPLE MID-SQUARE
i
Zi
Zi^2
Ui
0
7182
51581124
1
5811
33767721
0.5811
2
7677
58936329
0.7677
3
9363
87665769
0.9363
4
6657
44315649
0.6657
5
3156
9960336
0.3156
MID-SQUARE PROPERTIES



Once you know a Z, you can accurately predict
the entire future sequence (not really random)
If a Z ever repeats, the whole sequence starts
over
Only generate 9999 numbers (not dense in [0, 1]
Turns out, we LIKE some of these properties for
computer simulations (Repeatability enables
debugging)
DESIRABLE PROPERTIES

Appear Unif[0, 1]

Fast algorithm

Reproducible stream


Debugging

Contrast in comparison (Variance Reduction)
Lots of numbers before a repeat
PRELIM: MODULUS ARITHMETIC

mod is a mathematical operator


producing a result from two inputs (+, x, ^)
mod == “remainder upon division”

10 mod 6 = 4

12 mod 6 = 0

68 mod 14 = 56 mod 14 + 12 mod 14 = 12
LINEAR CONGRUENTIAL
GENERATOR (Lehmer, 1954)

Z0 is the SEED

m is the MODULUS

a is the MULTIPLIER

c is the INCREMENT
(forget this one)
U’s in (0, 1)
Z i  (aZ i 1  c) mod m
Zi
Ui 
m
PROPERTIES

Can generate at most m-1 samples before
repeat



Length of non-repeating sequence called the PERIOD
of the generator
If you get m-1, you have a full cycle generator
Divides [0, 1] into m equal slices
unif.xls


observe the basic functions of the seed,
multiplier, and modulus
experiment with multipliers for

m = 17

m = 16
HISTORY



Necessary for full cycle

a and m relatively prime

q (prime) divides m and a-1
m = 2,147,483,648 = 231-1 is everybody’s favorite 32-bit
generator (SIMAN, SIMSCRIPT, GPSS/H, Arena)
Fishman, G. S. (1972). An Exhaustive Study of Multipliers
for Modulus 231-1, RAND Technical Series.

a = 630,360,647
HISTORICAL COMPETITION FOR
LINEAR CONGRUENTIAL
GENERATORS
Zi  (a1Zi 1 a2 Zi 2  ...  an Zi n ) mod m

add or multiply some combination of
variates from the stream’s recent history
WHAT IS GOOD

Full, Long Cycle

Seemingly Independent

We can test this, but our simple tests stink
2
c
Test for U[0, 1]

U1, U2, ...Un a sequence of U[0, 1] samples

Let us divide [0, 1] into k equally-sized intervals

Let oi = observations in [(i-1)/k, i/k]

ei = n/k is the expected number of Ui’s that fall
in [(i-1)/k, i/k] for each i
c n 1
2
(oi  ei )

ei
2
TESTING


cn12 follows the Chi-Squared distribution with n1 degrees of freedom
DUMB TEST



any full-cycle generator is exactly AOK
expand to two or more dimensions using n- tuples
(Ui, Ui+1, ..., Ui+n)
maybe a picture would be better?