* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download vector. - cloudfront.net
Probability amplitude wikipedia , lookup
Dynamical system wikipedia , lookup
Hooke's law wikipedia , lookup
Fictitious force wikipedia , lookup
Derivations of the Lorentz transformations wikipedia , lookup
Cauchy stress tensor wikipedia , lookup
Equations of motion wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Photon polarization wikipedia , lookup
Minkowski space wikipedia , lookup
Work (physics) wikipedia , lookup
Tensor operator wikipedia , lookup
Velocity-addition formula wikipedia , lookup
Classical central-force problem wikipedia , lookup
Relativistic angular momentum wikipedia , lookup
Rigid body dynamics wikipedia , lookup
Bra–ket notation wikipedia , lookup
Laplace–Runge–Lenz vector wikipedia , lookup
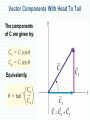
Two Dimensional Motion General Physics I Chapter 1: (1.7, 1.8) Vectors Motion in a Plane •Vector Addition •Velocity •Acceleration •Projectile motion •Relative Velocity Description • The previous section dealt mainly with motion whose path was a straight line. In real life though, many changes in direction are necessary unless you don’t want the motion to end prematurely. The motion whose path is a curved line is called curvilinear. • For simplicity, our world will be flat because we will consider only two out of the three dimensions: horizontal, vertical, and “depth”. Background Information • To study the motion on a curved path, we will apply a method which will allow us to reduce a curvilinear motion to two independent linear motions. • Let’s consider a curvilinear motion, like the path of a basket ball towards the hoop. Let’s say that the lighting of the arena is such that the ball will cast a “shadow” right underneath on the floor and another “shadow” right across on the wall behind the shooter. Background Information • v e r tic a l d i r e c ti o n B P y x O A horizontal direction • If you know where the shadows (projections) are, you can draw two perpendicular lines on the wall and find the ball at their intersection. In this way you could break down a curvilinear motion into a vertical motion and a horizontal motion and study the familiar linear motion of the shadows instead of the curvilinear motion of the ball. Therefore to describe the motion of the projections, you can use all the formulas from 1D Kinematics. Position Vector • In 2D Kinematics the location of the object is given by a pair of numbers like the horizontal distance x and the vertical distance y. • The distances are measured from a convenient point of reference to the projections of the object on the two directions. • In our example the point of reference O (also called origin) is at the intersection of the vertical and horizontal directions at the lower corner of the room: • OA = x and OB = y. Position Vector • r r • • θ • • • Another way to determine the location of the ball is by drawing an “oriented” segment from O to P conveniently represented by an arrow (you can imagine for example a laser beam originating in O and pointing at the ball). This arrow represents an extremely important notion in physics called vector. In this module we will use boldface letters to represent vectors, even though the traditional notation is a letter with a little arrow as a “hat”. In this particular case, the vector is called position vector and is denoted by the letter r. Any vector has two important characteristics: 1) magnitude or size, determined by the length of the arrow r and 2) direction, determined by the orientation of the vector usually given by an angle. In the example below, the angle θ is measured in relation to the horizontal direction. In short, the pair of numbers (r, θ) will completely “ID” the vector r. Vector Components • Let’s combine the information analyzed the previous example r r y θ x The two perpendicular lines from the tip of the vector r on the horizontal and vertical directions will mark two segments on these directions: x and y respectively. Using the same analogy as earlier, x and y would be the “shadows” (projections) of the vector r in appropriate lighting. The segments x and y are called the components of the vector r, and can be found using simple trigonometry. Since by definition cosine = adjacent/hypotenuse, we can write cosθ = x/r, therefore: x = r cosθ (1) Also by definition sine = opposite/hypotenuse, therefore sinθ = y/r and: y = r sinθ (2) Components • Components are numbers that can be added, subtracted, multiplied, etc… using the simple rules of arithmetic, whereas as you’ll see later, vectors have their own more complicated rules of “engagement” (operations). • Can we “restore” a vector if its components are given? Again, we need to do a little math to answer this question. By applying the Pythagorean Theorem in the right triangle above we get: • r2 = x2 + y2, or • r = √x2 + y2 (3) • Since by definition tangent = opposite/adjacent we can write: • tanθ = y/x, or • θ = arctan y/x (4) Components • To summarize, we can go back and forth between a vector and its components in the following ways: • From the vector r given by (r, θ) to the components x and y, use formulas (1) and (2). and, • From the components x and y to the vector r given by (r, θ), use formulas (3) and (4). • In conclusion, a vector can be denoted by a boldface letter followed by its magnitude and direction r(r, θ) or a boldface letter followed by its two components r(x, y). Vector Components General Projections of a vector on rectangular axis. Components are numbers A vector is determined by its components A (Ax, Ay) To find magnitude from components: y component of a vector opp hyp adj cos hyp sin opp tan cos adj sin A A A 2 x x component of a vector Find direction from components: arctan Ay Ax 2 y Example Components • Find the horizontal and vertical components of a position vector with the magnitude 4 m and direction 30o with the horizontal. x = r cosθ = 4 x cos 30 = 3.46 m y = r sinθ = 4 x sin 30 = 2 m (1) (2) Magnitude and Direction • Find the magnitude and direction of a position vector with the horizontal component 3m and the vertical component 4 m. r = √x2 + y2 = √32 + 42 = 5 m 5m (3) 4m θ = arctan y/x = θ = arctan 4/3 = 53.13o (4) 53.13o 3m Components Practice: Know (r, θ), find (x, y) 1) A fly is on the wall, at (3m, 36o) from the corner of the room (origin). Find x and y. x = 3 m x cos 36o = 2.43m y = 3m x sin 36o = 1.76 m 2) A bird flies with the velocity of 5.4 m/s, at an angle of 145o with the east direction (Ox axis). Find the x and y components of the velocity of the bird. vx = 5.4m/s x cos 145o = -4.42 m/s vy = 5.4 m/s x sin 145o = 3.10m/s 3) Find the components of the following acceleration vector of a plane: (17.3 m/s2, 200o). ax = 17.3 m/s2 x cos 200 = - 16.26 m/s2 ay = 17.3 x sin 200 = -5.92 m/s2 4) Find the components of the following force: (14.8 N, -64o) exerted by a shopper on the shopping cart. Fx = 14.8N x cos -64 = 6.49 N Fy = 14.8N x sin(-64) = -13.30N 5) The momentum of a rock is: 2.4 kg m/s, 77o. Find its components. px = 2.4 kg m/s x cos 77 = 0.54 kg m/s py = 2.4 kg m/s x sin 77 = 2.34 kg m/s Magnitude and Direction Practice Know (x, y) find (r, θ). 1) A fly is located on the wall at (4 m, 3 m) from the corner of the room. Find the magnitude and direction of the position vector of the insect. r = √42 + 32 = 5 m, θ = arctan ¾ = 36.86o 2) The components of the velocity of a bird are (-2 m/s, 5m/s). Find the magnitude and direction of its velocity vector. v = √-22 + 52 = 5.39 m, θ = arctan 5/-2 = -68.2o 3) The components of the acceleration of a plane are: (-4 m/s2, -2 m/s2). Find the corresponding acceleration vector. a = √-42 +- 22 = 4.47 m, θ = arctan -2/-4= 26.56o 4) Find the force whose components are: (0 N, -12 N) F = √02 + -122 = 12 N, θ = arctan -12/0= 270o 5) The momentum of a rock has the components: (4 kg m/s, -3 kg m/s). Find the momentum vector of the rock. p = √42 + -32 = 5 kg m/s, θ = arctan -3/4= -36.86o Vector Addition and Subtraction Addition of Perpendicular Vectors A is perpendicular to B, here is how to find C: Vector Addition Using Components • R=A+B 1) Find the components of each vector: A (Ax, Ay), B (Bx, By) 2) Add the like components: Rx = Ax + Bx, Ry = Ay + By 3) Restore the vector from its components: (Rx, Ry) (R, θ) Example 1: Vector A has a length of 5.00 meters and points along the x-axis. Vector B has a length of 3.00 meters and points 120 from the +x-axis. Compute A+B (=C). y B C 120 A x Example continued: opp sin hyp adj cos hyp sin opp tan cos adj y B By 60 Bx 120 A x Bx Bcos60 3.00m cos60 1.50 m B y B sin 60 3.00m sin 60 2.60 m and Ax = 5.00 m and Ay = 0.00 m Example continued: The components of C: C x Ax Bx 5.00 m 1.50 m 3.50 m C y Ay By 0.00 m 2.60 m 2.60 m y The length of C is: C C Cx C y C 2 Cy = 2.60 m Cx = 3.50 m 3.50 m 2 2.60 m 2 4.36 m x The direction of C is: tan 2 Cy Cx 2.60 m 0.7429 3.50 m tan 1 0.7429 36.6 From the +x-axis Example 2 Add the following velocities: (4.3 m/s, 5 m/s) + (-2 m/s, 2 m/s) = ( vx, vy) = (v, θ) (4.3 m/s, 5 m/s) + (-2 m/s, 2 m/s) = (2.3 m/s, 7 m/s) v = √2.32 + 72 = 7.37, θ = arctan 7/2.3 = 71.81o Diagram (2.3 m/s, 7 m/s) (4.3 m/s, 5 m/s) (-2 m/s, 2 m/s) Example 3 Add these velocities: (3.6 m/s, -3 m/s) + (-3.6 m/s, -3 m/s) = ( vx, vy) = (v, θ) (3.6 m/s, -3 m/s) + (-3.6 m/s, -3 m/s) = (0 m/s, -6 m/s) v = √02 + -62 = 6, θ = arctan 6/0 = 270o Diagram (-3.6 m/s, -3 m/s) (3.6 m/s, -3 m/s) (0 m/s, -6 m/s) Displacement Vector In 2D Kinematics displacement is a vector whose magnitude is the straightline distance from the initial to the final point of the motion. The direction points towards the final location of the object. Like mentioned in 1D Kinematics, the displacement is meant to describe the change in position, and is many times not the same as the distance traveled. Displacement Distance In the above diagram the straight line distance between A and B is the displacement and the curved line between A and B is the distance traveled. Adding Displacements Let’s consider now a situation in which a body makes two consecutive changes in position. For example, the dog in the picture below, first goes to feast on his bone, than to exercise a little after dinner, goes after the cat. According to definition, the final displacement of the dog is the straight line that joins D and C. Seems that we discovered a very important rule: how to add to displacements, and by extension two vectors that are placed “head to tail”. Geometric methods of vector addition Head To Tail (Triangle method): Rule: To add two vectors that are placed head to tail, join the origin of the first vector with the tip of the last vector. The resulting vector is called vector sum or resultant. This rule applies to any number of vectors. R = A +B Vector Components With Head To Tail The components of C are given by: Equivalently, Vector Addition and Subtraction The negative of a vector has the same magnitude but is opposite in direction to the original vector. Adding a negative vector is the same as subtracting a vector. Vector Addition Parallelogram Rule R=A+B R B A Example Component & Parallelogram Methods Add these velocities: ( 4 m/s, 35o) + ( 5 m/s, 120o) Ax = 4 m/s x cos 35 = 3.28 m/s, Ay = 4 m/s x sin 35 = 2.29 m/s Bx = 5 m/s x cos 120 = -2.5 m/s, By = 5 m/s x sin 120 = 4.33 m/s Rx = 3.28 + -2.5 = 0.78 m/s Ry = 2.29 + 4.33 = 6.62 m/s R = √0.782 + 6.622 = 6.67 m/s, θ = arctan 6.62/0.78 = 83.28 Diagram (6.67 m/s, 83.28o) (5 m/s, 120o) (4 m/s, 35o) (3.5, 90) + (10, 200) Ax = 0, Ay = 3.5 Bx = -9.4, By = -3.4 Rx = 0+-9.4 = -9.4, Ry = 3.5 + -3.4 = 0.1 R = 9.4 θ=-.61 Example Adding 3 Forces • (4N, 35o)+ (8N, 135o) + (7N,320o) Example Adding 3 Forces • • • • • • Rx = (4N)cos 35+(8N)cos 135+(7N) cos 320 Ry = (4N)sin 35+(8N)sin 135+(7N) sin 320 Rx = 2.98 Ry =3.45 R = √(Rx2 + Ry2) = √2.982 + 3.452)=4.56 θ = arctan Ry/Rx = arctan3.45/2.98 = 49.18o Example: Adding Two Velocities ► 15m/s Vector A B at 200o, 10 m/s at 110o Magnitude θ degrees θ radians Ax=Acosθ Ay=Asinθ -5.13 -14.10 3.49 200 15 9.40 -3.42 1.92 110 10 Ay=By Ax+Bx 4.27 -17.52 Ry Rx -17.52 R =sqrt(Rx^2+Ry^2) θ=arctan(Ry/Rx) 166.39 2.90 18.03 4.27 Add Two Velocities Diagram • Graphical Add Two Momentum Vectors Example ► 45000 Vector A B kg m/s@ 0o, 65000 kg m/s @ 45o Ay=Asinθ Ax=Acosθ Magnitude θ degrees θ radians 0.00 45000.00 0.00 0 45000 45961.94 45961.94 0.79 45 65000 Ay+By Ax+Bx 45961.94 90961.94 R =sqrt(Rx^2+Ry^2) Ry Rx 101914.55 90961.94 45961.94 θ=arctan(Ry/Rx) 0.47 26.82 Add Two Momentum Vectors Graphical Method Add 3 Force Vectors (2) ► 750 N @ 270, 450 N @ 45, 200 N @ 135 Vector A B C Magnitude θ degrees θ radians Ax=Acosθ Ay=Asinθ -750.00 0.00 4.71 270 750 318.20 318.20 0.79 45 450 141.42 -141.42 2.36 135 200 Ax+Bx+Cx 176.78 Ry Rx 176.78 Ay+By+Cy -290.38 R =sqrt(Rx^2+Ry^2) θ=arctan(Ry/Rx) -58.70 -1.02 339.96 -290.38 Add 3 Force Vectors Graphically (2) Add 3 Acceleration Vectors ► 9.8 m/s2 @270, 14.8 m/s2 @ 105, 2.4 m/s2 @20 Vector A B C Magnitude θ degrees θ radians Ax=Acosθ Ay=Asinθ -9.80 0.00 4.71 270 9.8 14.30 -3.83 1.83 105 14.8 0.82 2.26 0.35 20 2.4 Ax+Bx+Cx -1.58 Ry Rx -1.58 Ay+By+Cy 5.32 R =sqrt(Rx^2+Ry^2) θ=arctan(Ry/Rx) 106.56 1.86 5.55 5.32 Add 3 Acceleration Vectors Graph • Graph Boat vbr = 3m/s velocity of boat in relation with the river (water) vrs = 1m/s velocity of river in relation with the shore Boat vbs= √(vbr2 + vrs2) √(3m/s)2 + (1m/s )2 = 3.16 m/s velocity of boat in relation with the shore tan θ = vrs/vbr = 1/3 θ =arctan 1/3 = 18.43o Relative Velocity In two dimensions, the components of the velocity, and therefore the angle it makes with a coordinate axis, will change depending on the point of view. vbr = 3m/s velocity of boat in relation with the river (water) vrs = 1m/s velocity of river in relation with the shore vbs= √(vbr2 + vrs2) √(3m/s)2 + (1m/s )2 = 3.16 m/s velocity of boat in relation with the shore tan θ = vrs/vbr = 1/3 θ =arctan 1/3 = 18.43o θ ConcepTest 3.1a If two vectors are given Vectors I 1) same magnitude, but can be in any direction such that A + B = 0, what 2) same magnitude, but must be in the same direction can you say about the magnitude and direction of vectors A and B? 3) different magnitudes, but must be in the same direction 4) same magnitude, but must be in opposite directions 5) different magnitudes, but must be in opposite directions ConcepTest 3.1a If two vectors are given Vectors I 1) same magnitude, but can be in any direction such that A + B = 0, what 2) same magnitude, but must be in the same direction can you say about the magnitude and direction of vectors A and B? 3) different magnitudes, but must be in the same direction 4) same magnitude, but must be in opposite directions 5) different magnitudes, but must be in opposite directions The magnitudes must be the same, but one vector must be pointing in the opposite direction of the other in order for the sum to come out to zero. You can prove this with the tip-to-tail method. ConcepTest 3.1b Vectors II Given that A + B = C, and 1) they are perpendicular to each other 2) they are parallel and in the same direction that lAl 2 + lBl 2 = lCl 2, how are vectors A and B 3) they are parallel but in the opposite oriented with respect to direction each other? 4) they are at 45° to each other 5) they can be at any angle to each other ConcepTest 3.1b Vectors II Given that A + B = C, and 1) they are perpendicular to each other 2) they are parallel and in the same direction that lAl 2 + lBl 2 = lCl 2, how are vectors A and B 3) they are parallel but in the opposite oriented with respect to direction each other? 4) they are at 45° to each other 5) they can be at any angle to each other Note that the magnitudes of the vectors satisfy the Pythagorean theorem. This suggests that they form a right triangle, with vector C as the hypotenuse. Thus, A and B are the legs of the right triangle and are therefore perpendicular. ConcepTest 3.1c Given that A + B = C, and that lAl + lBl = lCl , how are vectors A and B oriented with respect to each other? Vectors III 1) they are perpendicular to each other 2) they are parallel and in the same direction 3) they are parallel but in the opposite direction 4) they are at 45° to each other 5) they can be at any angle to each other ConcepTest 3.1c Given that A + B = C, and that lAl + lBl = lCl , how are vectors A and B oriented with respect to each other? Vectors III 1) they are perpendicular to each other 2) they are parallel and in the same direction 3) they are parallel but in the opposite direction 4) they are at 45° to each other 5) they can be at any angle to each other The only time vector magnitudes will simply add together is when the direction does not have to be taken into account (i.e., the direction is the same for both vectors). In that case, there is no angle between them to worry about, so vectors A and B must be pointing in the same direction. ConcepTest 3.2a Vector Components I 1) it doubles If each component of a vector is doubled, what happens to the angle of that vector? 2) it increases, but by less than double 3) it does not change 4) it is reduced by half 5) it decreases, but not as much as half ConcepTest 3.2a Vector Components I 1) it doubles If each component of a vector is doubled, what happens to the angle of that vector? 2) it increases, but by less than double 3) it does not change 4) it is reduced by half 5) it decreases, but not as much as half The magnitude of the vector clearly doubles if each of its components is doubled. But the angle of the vector is given by tan = 2y/2x, which is the same as tan = y/x (the original angle). Follow-up: If you double one component and not the other, how would the angle change? ConcepTest 3.2b Vector Components II A certain vector has x and y components that are equal in magnitude. Which of the following is a possible angle for this vector in a standard x-y coordinate system? 1) 30° 2) 180° 3) 90° 4) 60° 5) 45° ConcepTest 3.2b Vector Components II A certain vector has x and y components that are equal in magnitude. Which of the following is a possible angle for this vector in a standard x-y coordinate system? 1) 30° 2) 180° 3) 90° 4) 60° 5) 45° The angle of the vector is given by tan = y/x. Thus, tan = 1 in this case if x and y are equal, which means that the angle must be 45°. ConcepTest 3.3 Vector Addition You are adding vectors of length 1) 0 20 and 40 units. What is the only 2) 18 possible resultant magnitude that 3) 37 you can obtain out of the 4) 64 following choices? 5) 100 ConcepTest 3.3 Vector Addition You are adding vectors of length 1) 0 20 and 40 units. What is the only 2) 18 possible resultant magnitude that 3) 37 you can obtain out of the 4) 64 following choices? 5) 100 The minimum resultant occurs when the vectors are opposite, giving 20 units. The maximum resultant occurs when the vectors are aligned, giving 60 units. Anything in between is also possible for angles between 0° and 180°. ConcepTest 3.4a A small cart is rolling at constant velocity on a flat track. It fires a ball straight up into the air as it moves. After it is fired, what happens to the ball? Firing Balls I 1) it depends on how fast the cart is moving 2) it falls behind the cart 3) it falls in front of the cart 4) it falls right back into the cart 5) it remains at rest ConcepTest 3.4a A small cart is rolling at constant velocity on a flat track. It fires a ball straight up into the air as it moves. After it is fired, what happens to the ball? In the frame of reference of the cart, the ball only has a vertical component of velocity. So it goes up and comes back down. To a ground observer, both the cart and the ball have the same horizontal velocity, so the ball still returns into the cart. Firing Balls I 1) it depends on how fast the cart is moving 2) it falls behind the cart 3) it falls in front of the cart 4) it falls right back into the cart 5) it remains at rest when viewed from train when viewed from ground ConcepTest 3.4b Now the cart is being pulled along a horizontal track by an external force (a weight hanging over the table edge) and accelerating. It fires a ball straight out of the cannon as it moves. After it is fired, what happens to the ball? Firing Balls II 1) it depends upon how much the track is tilted 2) it falls behind the cart 3) it falls in front of the cart 4) it falls right back into the cart 5) it remains at rest ConcepTest 3.4b Now the cart is being pulled along a horizontal track by an external force (a weight hanging over the table edge) and accelerating. It fires a ball straight out of the cannon as it moves. After it is fired, what happens to the ball? Firing Balls II 1) it depends upon how much the track is tilted 2) it falls behind the cart 3) it falls in front of the cart 4) it falls right back into the cart 5) it remains at rest Now the acceleration of the cart is completely unrelated to the ball. In fact, the ball does not have any horizontal acceleration at all (just like the first question), so it will lag behind the accelerating cart once it is shot out of the cannon. ConcepTest 3.4c The same small cart is now rolling down an inclined track and accelerating. It fires a ball straight out of the cannon as it moves. After it is fired, what happens to the ball? Firing Balls III 1) it depends upon how much the track is tilted 2) it falls behind the cart 3) it falls in front of the cart 4) it falls right back into the cart 5) it remains at rest ConcepTest 3.4c The same small cart is now rolling down an inclined track and accelerating. It fires a ball straight out of the cannon as it moves. After it is fired, what happens to the ball? Firing Balls III 1) it depends upon how much the track is tilted 2) it falls behind the cart 3) it falls in front of the cart 4) it falls right back into the cart 5) it remains at rest Because the track is inclined, the cart accelerates. However, the ball has the same component of acceleration along the track as the cart does! This is essentially the component of g acting parallel to the inclined track. So the ball is effectively accelerating down the incline, just as the cart is, and it falls back into the cart. Review A person walks the path shown. The total trip consists of four straight-line paths. In the box provided give the X and Y components of each vector. (round up to the nearest integer) ► 3. A(12m, 270o) D(8m, 30o) C(20m, 0o) X A B C B(10m, 135o) D R y Review A person walks the path shown. The total trip consists of four straight-line paths. y In the box provided give the X and Y components of each vector (round up to the nearest integer) ► 3. A(12m, 270o) C(20m, 0) D(8m, 30) B(10m, 135o) O x X y A 0 -12 B -7 7 C 20 0 D 7 4 R 20 -1