Download vector. - cloudfront.net

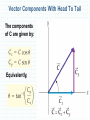
Two Dimensional Motion
General Physics I
Chapter 1: (1.7, 1.8) Vectors
Motion in a Plane
•Vector Addition
•Velocity
•Acceleration
•Projectile motion
•Relative Velocity
Description
• The previous section dealt mainly with motion
whose path was a straight line. In real life
though, many changes in direction are
necessary unless you don’t want the motion to
end prematurely. The motion whose path is a
curved line is called curvilinear.
• For simplicity, our world will be flat because we
will consider only two out of the three
dimensions: horizontal, vertical, and “depth”.
Background Information
• To study the motion on a curved path, we will
apply a method which will allow us to reduce a
curvilinear motion to two independent linear
motions.
• Let’s consider a curvilinear motion, like the path
of a basket ball towards the hoop. Let’s say that
the lighting of the arena is such that the ball will
cast a “shadow” right underneath on the floor
and another “shadow” right across on the wall
behind the shooter.
Background Information
•
v
e
r
tic
a
l
d
i
r
e
c
ti
o
n
B
P
y
x
O
A
horizontal direction
•
If you know where the
shadows (projections)
are, you can draw two
perpendicular lines on
the wall and find the
ball at their
intersection. In this
way you could break
down a curvilinear
motion into a vertical
motion and a
horizontal motion and
study the familiar
linear motion of the
shadows instead of the
curvilinear motion of
the ball.
Therefore to describe
the motion of the
projections, you can
use all the formulas
from 1D Kinematics.
Position Vector
• In 2D Kinematics the location of the object is given by a
pair of numbers like the horizontal distance x and the
vertical distance y.
• The distances are measured from a convenient point of
reference to the projections of the object on the two
directions.
• In our example the point of reference O (also called
origin) is at the intersection of the vertical and horizontal
directions at the lower corner of the room:
• OA = x and OB = y.
Position Vector
•
r
r
•
•
θ
•
•
•
Another way to determine the location of the ball
is by drawing an “oriented” segment from O to P
conveniently represented by an arrow (you can
imagine for example a laser beam originating in
O and pointing at the ball).
This arrow represents an extremely important
notion in physics called vector. In this module
we will use boldface letters to represent vectors,
even though the traditional notation is a letter
with a little arrow as a “hat”.
In this particular case, the vector is called
position vector and is denoted by the letter r.
Any vector has two important characteristics:
1) magnitude or size, determined by the length
of the arrow r and
2) direction, determined by the orientation of the
vector usually given by an angle. In the example
below, the angle θ is measured in relation to the
horizontal direction.
In short, the pair of numbers (r, θ) will
completely “ID” the vector r.
Vector Components
• Let’s combine the information analyzed the previous example
r
r
y
θ
x
The two perpendicular lines from the tip of the
vector r on the horizontal and vertical directions will
mark two segments on these directions: x and y
respectively. Using the same analogy as earlier, x
and y would be the “shadows” (projections) of the
vector r in appropriate lighting.
The segments x and y are called the components of
the vector r, and can be found using simple
trigonometry.
Since by definition cosine = adjacent/hypotenuse,
we can write cosθ = x/r, therefore:
x = r cosθ
(1)
Also by definition sine = opposite/hypotenuse,
therefore sinθ = y/r and:
y = r sinθ
(2)
Components
• Components are numbers that can be added, subtracted, multiplied,
etc… using the simple rules of arithmetic, whereas as you’ll see
later, vectors have their own more complicated rules of
“engagement” (operations).
• Can we “restore” a vector if its components are given? Again, we
need to do a little math to answer this question. By applying the
Pythagorean Theorem in the right triangle above we get:
•
r2 = x2 + y2, or
•
r = √x2 + y2
(3)
• Since by definition tangent = opposite/adjacent we can write:
•
tanθ = y/x, or
•
θ = arctan y/x
(4)
Components
• To summarize, we can go back and forth
between a vector and its components in the
following ways:
• From the vector r given by (r, θ) to the
components x and y, use formulas (1) and (2).
and,
• From the components x and y to the vector r
given by (r, θ), use formulas (3) and (4).
• In conclusion, a vector can be denoted by a
boldface letter followed by its magnitude and
direction r(r, θ) or a boldface letter followed by
its two components r(x, y).
Vector Components General
Projections of a vector on rectangular axis.
Components are numbers
A vector is
determined by its
components
A (Ax, Ay)
To find magnitude
from components:
y component
of a vector
opp
hyp
adj
cos 
hyp
sin  opp
tan  

cos adj
sin  
A A  A
2
x
x component
of a vector
Find direction from components:
  arctan
Ay
Ax
2
y
Example Components
• Find the horizontal and vertical components of a
position vector with the magnitude 4 m and
direction 30o with the horizontal.
x = r cosθ = 4 x cos 30 = 3.46 m
y = r sinθ = 4 x sin 30 = 2 m
(1)
(2)
Magnitude and Direction
• Find the magnitude and direction of a
position vector with the horizontal
component 3m and the vertical component 4
m.
r = √x2 + y2 = √32 + 42 = 5 m
5m
(3)
4m
θ = arctan y/x = θ = arctan 4/3 = 53.13o
(4)
53.13o
3m
Components Practice: Know (r, θ), find (x, y)
1) A fly is on the wall, at (3m, 36o) from the corner of the room
(origin). Find x and y.
x = 3 m x cos 36o = 2.43m
y = 3m x sin 36o = 1.76 m
2) A bird flies with the velocity of 5.4 m/s, at an angle of 145o with the east
direction (Ox axis). Find the x and y components of the velocity of the bird.
vx = 5.4m/s x cos 145o = -4.42 m/s vy = 5.4 m/s x sin 145o = 3.10m/s
3) Find the components of the following acceleration vector of a plane:
(17.3 m/s2, 200o).
ax = 17.3 m/s2 x cos 200 = - 16.26 m/s2 ay = 17.3 x sin 200 = -5.92 m/s2
4) Find the components of the following force: (14.8 N, -64o)
exerted by a shopper on the shopping cart.
Fx = 14.8N x cos -64 = 6.49 N Fy = 14.8N x sin(-64) = -13.30N
5) The momentum of a rock is: 2.4 kg m/s, 77o. Find its components.
px = 2.4 kg m/s x cos 77 = 0.54 kg m/s
py = 2.4 kg m/s x sin 77 = 2.34 kg m/s
Magnitude and Direction Practice
Know (x, y) find (r, θ).
1) A fly is located on the wall at (4 m, 3 m) from the corner of the room. Find
the magnitude and direction of the position vector of the insect.
r = √42 + 32 = 5 m,
θ = arctan ¾ = 36.86o
2) The components of the velocity of a bird are (-2 m/s, 5m/s). Find
the magnitude and direction of its velocity vector.
v = √-22 + 52 = 5.39 m,
θ = arctan 5/-2 = -68.2o
3) The components of the acceleration of a plane are: (-4 m/s2, -2 m/s2).
Find the corresponding acceleration vector.
a = √-42 +- 22 = 4.47 m,
θ = arctan -2/-4= 26.56o
4) Find the force whose components are: (0 N, -12 N)
F = √02 + -122 = 12 N,
θ = arctan -12/0= 270o
5) The momentum of a rock has the components: (4 kg m/s, -3 kg m/s).
Find the momentum vector of the rock.
p = √42 + -32 = 5 kg m/s,
θ = arctan -3/4= -36.86o
Vector Addition and Subtraction
Addition of Perpendicular Vectors
A is perpendicular to
B, here is how to find
C:
Vector Addition Using Components
• R=A+B
1) Find the components of each vector:
A
(Ax, Ay), B
(Bx, By)
2) Add the like components:
Rx = Ax + Bx,
Ry = Ay + By
3) Restore the vector from its components:
(Rx, Ry)
(R, θ)
Example 1: Vector A has a length of 5.00 meters and points
along the x-axis. Vector B has a length of 3.00 meters and
points 120 from the +x-axis. Compute A+B (=C).
y
B
C
120
A
x
Example continued:
opp
sin  
hyp
adj
cos 
hyp
sin  opp
tan  

cos adj
y
B
By
60
Bx
120
A
x
Bx   Bcos60  3.00m cos60  1.50 m
B y  B sin 60  3.00m sin 60  2.60 m
and Ax = 5.00 m and Ay = 0.00 m
Example continued:
The components of C:
C x  Ax  Bx  5.00 m   1.50 m   3.50 m
C y  Ay  By  0.00 m  2.60 m  2.60 m
y
The length of C is:
C  C  Cx  C y
C
2
Cy = 2.60 m


Cx = 3.50 m
3.50 m 2  2.60 m 2
 4.36 m
x
The direction of C is: tan  
2
Cy
Cx

2.60 m
 0.7429
3.50 m
  tan 1 0.7429  36.6
From the +x-axis
Example 2
Add the following velocities:
(4.3 m/s, 5 m/s) + (-2 m/s, 2 m/s) = ( vx, vy) = (v, θ)
(4.3 m/s, 5 m/s) + (-2 m/s, 2 m/s) = (2.3 m/s, 7 m/s)
v = √2.32 + 72 = 7.37, θ = arctan 7/2.3 = 71.81o
Diagram
(2.3 m/s, 7 m/s)
(4.3 m/s, 5 m/s)
(-2 m/s, 2 m/s)
Example 3
Add these velocities:
(3.6 m/s, -3 m/s) + (-3.6 m/s, -3 m/s) = ( vx, vy) = (v, θ)
(3.6 m/s, -3 m/s) + (-3.6 m/s, -3 m/s) = (0 m/s, -6 m/s)
v = √02 + -62 = 6,
θ = arctan 6/0 = 270o
Diagram
(-3.6 m/s, -3 m/s)
(3.6 m/s, -3 m/s)
(0 m/s, -6 m/s)
Displacement Vector
In 2D Kinematics displacement is a vector whose magnitude is the straightline distance from the initial to the final point of the motion. The direction
points towards the final location of the object.
Like mentioned in 1D Kinematics, the displacement is meant to describe the
change in position, and is many times not the same as the distance traveled.
Displacement
Distance
In the above diagram the straight line distance between A and
B is the displacement and the curved line between A and B is
the distance traveled.
Adding Displacements
Let’s consider now a situation in which a body makes two consecutive
changes in position.
For example, the dog in the picture below, first goes to feast on his
bone, than to exercise a little after dinner, goes after the cat.
According to definition, the final displacement of the dog is the straight
line that joins D and C. Seems that we discovered a very important rule:
how to add to displacements, and by extension two vectors that are
placed “head to tail”.
Geometric methods of vector addition
Head To Tail (Triangle method):
Rule: To add two vectors that are placed head to tail, join the origin of
the first vector with the tip of the last vector. The resulting vector is called
vector sum or resultant. This rule applies to any number of vectors.
R = A +B
Vector Components With Head To Tail
The components
of C are given by:
Equivalently,
Vector Addition and Subtraction
The negative of a vector has the same
magnitude but is opposite in direction to the
original vector. Adding a negative vector is the
same as subtracting a vector.
Vector Addition Parallelogram Rule
R=A+B
R
B
A
Example Component &
Parallelogram Methods
Add these velocities: ( 4 m/s, 35o) + ( 5 m/s, 120o)
Ax = 4 m/s x cos 35 = 3.28 m/s, Ay = 4 m/s x sin 35 = 2.29 m/s
Bx = 5 m/s x cos 120 = -2.5 m/s, By = 5 m/s x sin 120 = 4.33 m/s
Rx = 3.28 + -2.5 = 0.78 m/s
Ry = 2.29 + 4.33 = 6.62 m/s
R = √0.782 + 6.622 = 6.67 m/s, θ = arctan 6.62/0.78 = 83.28
Diagram
(6.67 m/s, 83.28o)
(5 m/s, 120o)
(4 m/s, 35o)
(3.5, 90) + (10, 200)
Ax = 0, Ay = 3.5
Bx = -9.4, By = -3.4
Rx = 0+-9.4 = -9.4, Ry = 3.5 + -3.4 = 0.1
R = 9.4
θ=-.61
Example Adding 3 Forces
• (4N, 35o)+ (8N, 135o) + (7N,320o)
Example Adding 3 Forces
•
•
•
•
•
•
Rx = (4N)cos 35+(8N)cos 135+(7N) cos 320
Ry = (4N)sin 35+(8N)sin 135+(7N) sin 320
Rx = 2.98
Ry =3.45
R = √(Rx2 + Ry2) = √2.982 + 3.452)=4.56
θ = arctan Ry/Rx = arctan3.45/2.98 = 49.18o
Example: Adding Two Velocities
► 15m/s
Vector
A
B
at 200o, 10 m/s at 110o
Magnitude θ degrees θ radians Ax=Acosθ Ay=Asinθ
-5.13
-14.10
3.49
200
15
9.40
-3.42
1.92
110
10
Ay=By
Ax+Bx
4.27
-17.52
Ry
Rx
-17.52
R =sqrt(Rx^2+Ry^2) θ=arctan(Ry/Rx)
166.39
2.90
18.03
4.27
Add Two Velocities Diagram
• Graphical
Add Two Momentum Vectors
Example
► 45000
Vector
A
B
kg m/s@ 0o, 65000 kg m/s @ 45o
Ay=Asinθ
Ax=Acosθ
Magnitude θ degrees θ radians
0.00
45000.00
0.00
0
45000
45961.94
45961.94
0.79
45
65000
Ay+By
Ax+Bx
45961.94
90961.94
R =sqrt(Rx^2+Ry^2)
Ry
Rx
101914.55
90961.94 45961.94
θ=arctan(Ry/Rx)
0.47
26.82
Add Two Momentum Vectors
Graphical Method
Add 3 Force Vectors (2)
►
750 N @ 270, 450 N @ 45, 200 N @ 135
Vector
A
B
C
Magnitude θ degrees θ radians Ax=Acosθ Ay=Asinθ
-750.00
0.00
4.71
270
750
318.20
318.20
0.79
45
450
141.42
-141.42
2.36
135
200
Ax+Bx+Cx
176.78
Ry
Rx
176.78
Ay+By+Cy
-290.38
R =sqrt(Rx^2+Ry^2) θ=arctan(Ry/Rx)
-58.70
-1.02
339.96
-290.38
Add 3 Force Vectors Graphically
(2)
Add 3 Acceleration Vectors
►
9.8 m/s2 @270, 14.8 m/s2 @ 105, 2.4 m/s2 @20
Vector
A
B
C
Magnitude θ degrees θ radians Ax=Acosθ Ay=Asinθ
-9.80
0.00
4.71
270
9.8
14.30
-3.83
1.83
105
14.8
0.82
2.26
0.35
20
2.4
Ax+Bx+Cx
-1.58
Ry
Rx
-1.58
Ay+By+Cy
5.32
R =sqrt(Rx^2+Ry^2) θ=arctan(Ry/Rx)
106.56
1.86
5.55
5.32
Add 3 Acceleration Vectors Graph
• Graph
Boat
vbr = 3m/s velocity of
boat in relation with
the river (water)
vrs = 1m/s velocity of
river in relation with
the shore
Boat
vbs= √(vbr2 + vrs2)
√(3m/s)2 + (1m/s )2 =
3.16 m/s velocity of
boat in relation with
the shore
tan θ = vrs/vbr = 1/3
θ =arctan 1/3 = 18.43o
Relative Velocity
In two dimensions, the components of the velocity, and
therefore the angle it makes with a coordinate axis, will
change depending on the point of view.
vbr = 3m/s velocity of
boat in relation with
the river (water)
vrs = 1m/s velocity of
river in relation with
the shore
vbs= √(vbr2 + vrs2)
√(3m/s)2 + (1m/s )2 =
3.16 m/s velocity of
boat in relation with
the shore
tan θ = vrs/vbr = 1/3
θ =arctan 1/3 = 18.43o
θ
ConcepTest 3.1a
If two vectors are given
Vectors I
1) same magnitude, but can be in any
direction
such that A + B = 0, what 2) same magnitude, but must be in the same
direction
can you say about the
magnitude and direction
of vectors A and B?
3) different magnitudes, but must be in the
same direction
4) same magnitude, but must be in opposite
directions
5) different magnitudes, but must be in
opposite directions
ConcepTest 3.1a
If two vectors are given
Vectors I
1) same magnitude, but can be in any
direction
such that A + B = 0, what 2) same magnitude, but must be in the same
direction
can you say about the
magnitude and direction
of vectors A and B?
3) different magnitudes, but must be in the
same direction
4) same magnitude, but must be in opposite
directions
5) different magnitudes, but must be in
opposite directions
The magnitudes must be the same, but one vector must be pointing in
the opposite direction of the other in order for the sum to come out to
zero. You can prove this with the tip-to-tail method.
ConcepTest 3.1b
Vectors II
Given that A + B = C, and 1) they are perpendicular to each other
2) they are parallel and in the same direction
that lAl 2 + lBl 2 = lCl 2,
how are vectors A and B 3) they are parallel but in the opposite
oriented with respect to
direction
each other?
4) they are at 45° to each other
5) they can be at any angle to each other
ConcepTest 3.1b
Vectors II
Given that A + B = C, and 1) they are perpendicular to each other
2) they are parallel and in the same direction
that lAl 2 + lBl 2 = lCl 2,
how are vectors A and B 3) they are parallel but in the opposite
oriented with respect to
direction
each other?
4) they are at 45° to each other
5) they can be at any angle to each other
Note that the magnitudes of the vectors satisfy the Pythagorean
theorem. This suggests that they form a right triangle, with vector C
as the hypotenuse. Thus, A and B are the legs of the right triangle and
are therefore perpendicular.
ConcepTest 3.1c
Given that A + B = C,
and that lAl + lBl =
lCl , how are vectors
A and B oriented with
respect to each
other?
Vectors III
1) they are perpendicular to each other
2) they are parallel and in the same direction
3) they are parallel but in the opposite direction
4) they are at 45° to each other
5) they can be at any angle to each other
ConcepTest 3.1c
Given that A + B = C,
and that lAl + lBl =
lCl , how are vectors
A and B oriented with
respect to each
other?
Vectors III
1) they are perpendicular to each other
2) they are parallel and in the same direction
3) they are parallel but in the opposite direction
4) they are at 45° to each other
5) they can be at any angle to each other
The only time vector magnitudes will simply add together is when the
direction does not have to be taken into account (i.e., the direction is
the same for both vectors). In that case, there is no angle between
them to worry about, so vectors A and B must be pointing in the
same direction.
ConcepTest 3.2a
Vector Components I
1) it doubles
If each component of a
vector is doubled, what
happens to the angle of
that vector?
2) it increases, but by less than double
3) it does not change
4) it is reduced by half
5) it decreases, but not as much as half
ConcepTest 3.2a
Vector Components I
1) it doubles
If each component of a
vector is doubled, what
happens to the angle of
that vector?
2) it increases, but by less than double
3) it does not change
4) it is reduced by half
5) it decreases, but not as much as half
The magnitude of the vector clearly doubles if each of its
components is doubled. But the angle of the vector is given by tan
 = 2y/2x, which is the same as tan  = y/x (the original angle).
Follow-up: If you double one component and not
the other, how would the angle change?
ConcepTest 3.2b
Vector Components II
A certain vector has x and y components
that are equal in magnitude. Which of the
following is a possible angle for this vector
in a standard x-y coordinate system?
1) 30°
2) 180°
3) 90°
4) 60°
5) 45°
ConcepTest 3.2b
Vector Components II
A certain vector has x and y components
that are equal in magnitude. Which of the
following is a possible angle for this vector
in a standard x-y coordinate system?
1) 30°
2) 180°
3) 90°
4) 60°
5) 45°
The angle of the vector is given by tan  = y/x. Thus, tan  = 1
in this case if x and y are equal, which means that the angle
must be 45°.
ConcepTest 3.3
Vector Addition
You are adding vectors of length
1) 0
20 and 40 units. What is the only
2) 18
possible resultant magnitude that
3) 37
you can obtain out of the
4) 64
following choices?
5) 100
ConcepTest 3.3
Vector Addition
You are adding vectors of length
1) 0
20 and 40 units. What is the only
2) 18
possible resultant magnitude that
3) 37
you can obtain out of the
4) 64
following choices?
5) 100
The minimum resultant occurs when the vectors
are opposite, giving 20 units. The maximum
resultant occurs when the vectors are aligned,
giving 60 units. Anything in between is also
possible for angles between 0° and 180°.
ConcepTest 3.4a
A small cart is rolling at
constant velocity on a flat
track. It fires a ball straight
up into the air as it moves.
After it is fired, what happens
to the ball?
Firing Balls I
1) it depends on how fast the cart is
moving
2) it falls behind the cart
3) it falls in front of the cart
4) it falls right back into the cart
5) it remains at rest
ConcepTest 3.4a
A small cart is rolling at
constant velocity on a flat
track. It fires a ball straight
up into the air as it moves.
After it is fired, what happens
to the ball?
In the frame of reference of
the cart, the ball only has a
vertical component of
velocity. So it goes up and
comes back down. To a
ground observer, both the
cart and the ball have the
same horizontal velocity,
so the ball still returns into
the cart.
Firing Balls I
1) it depends on how fast the cart is
moving
2) it falls behind the cart
3) it falls in front of the cart
4) it falls right back into the cart
5) it remains at rest
when
viewed from
train
when
viewed from
ground
ConcepTest 3.4b
Now the cart is being pulled
along a horizontal track by an
external force (a weight
hanging over the table edge)
and accelerating. It fires a ball
straight out of the cannon as it
moves. After it is fired, what
happens to the ball?
Firing Balls II
1) it depends upon how much the
track is tilted
2) it falls behind the cart
3) it falls in front of the cart
4) it falls right back into the cart
5) it remains at rest
ConcepTest 3.4b
Now the cart is being pulled
along a horizontal track by an
external force (a weight
hanging over the table edge)
and accelerating. It fires a ball
straight out of the cannon as it
moves. After it is fired, what
happens to the ball?
Firing Balls II
1) it depends upon how much the
track is tilted
2) it falls behind the cart
3) it falls in front of the cart
4) it falls right back into the cart
5) it remains at rest
Now the acceleration of the cart is completely unrelated to the ball. In
fact, the ball does not have any horizontal acceleration at all (just like
the first question), so it will lag behind the accelerating cart once it is
shot out of the cannon.
ConcepTest 3.4c
The same small cart is
now rolling down an
inclined track and
accelerating. It fires a
ball straight out of the
cannon as it moves.
After it is fired, what
happens to the ball?
Firing Balls III
1) it depends upon how much the track is tilted
2) it falls behind the cart
3) it falls in front of the cart
4) it falls right back into the cart
5) it remains at rest
ConcepTest 3.4c
The same small cart is
now rolling down an
inclined track and
accelerating. It fires a
ball straight out of the
cannon as it moves.
After it is fired, what
happens to the ball?
Firing Balls III
1) it depends upon how much the track is tilted
2) it falls behind the cart
3) it falls in front of the cart
4) it falls right back into the cart
5) it remains at rest
Because the track is inclined, the cart accelerates. However, the ball
has the same component of acceleration along the track as the cart
does! This is essentially the component of g acting parallel to the
inclined track. So the ball is effectively accelerating down the incline,
just as the cart is, and it falls back into the cart.
Review
A person walks
the path shown. The
total trip consists of
four straight-line
paths.
In the box provided
give the X and Y
components of each
vector. (round up to
the nearest integer)
► 3.
A(12m, 270o)
D(8m, 30o)
C(20m, 0o)
X
A
B
C
B(10m, 135o)
D
R
y
Review
A person walks
the path shown. The
total trip consists of
four straight-line
paths. y
In the box provided
give the X and Y
components of
each vector (round
up to the nearest
integer)
► 3.
A(12m, 270o)
C(20m, 0)
D(8m, 30)
B(10m, 135o)
O
x
X
y
A
0
-12
B
-7
7
C
20
0
D
7
4
R
20
-1