Download Ch18 links

Ch18 links / ch18 pdf links
Ch18 image
t-dist table with 38 df / 30 df
t-dist table
/ 20 df
ch18 (inference about population mean)
exercises: 18.3, 18.5, 18.7, 18.9, 18.15, 18.17, 18.19, 18.27
18.17 You are testing H0: μ = 100 against Ha: μ < 100 based on an
SRS of 25 observations from a Normal population. The t statistic
is t = −2.5. The degrees of freedom for the t statistic are
(a) 26.
(b) 25.
(c) 24.
Answer
(c) df = 25 − 1 = 24.
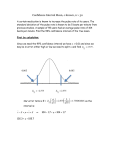
18.3 Critical values. Use Table C or software to find
(a) the critical value for a one-sided test with level = 0.05 based on the t(4) distribution.
(b) the critical value for a 98% confidence interval based on the t(26) distribution.
Answer
(a) t* = 2.132. (b) t* = 2.479.
18.5 Critical values. What critical value t* from Table C would you use for
a confidence interval for the mean of the population in each of the following
situations?
(a) A 95% confidence interval based on n = 12 observations.
(b) A 99% confidence interval from an SRS of 18 observations.
(c) A 90% confidence interval from a sample of size 6.
Answer
(a) df = 12 − 1 = 11, so t* = 2.201.
(b) df = 18 − 1 = 17, so t* = 2.898.
(c) df = 6 − 1 = 5, so t* = 2.015
18.7 Ancient air. The composition of the earth’s atmosphere may have
changed over time. To try to discover the nature of the atmosphere long
ago, we can examine the gas in bubbles inside ancient amber. Amber is tree
resin that has hardened and been trapped in rocks. The gas in bubbles
within amber should be a sample of the atmosphere at the time the amber
was formed. Measurements on specimens of amber from the late Cretaceous
era (75 to 95 million years ago) give these percents of nitrogen:
Assume (this is not yet agreed on by experts) that these observations are an
SRS from the late Cretaceous atmosphere. Use a 90% confidence interval to
estimate the mean percent of nitrogen in ancient air. Follow the four-step
process as illustrated in Example 18.2. (Our present-day atmosphere is
about 78.1% nitrogen.)
Answer
We are told to view the observations as an SRS. A stemplot shows some
left-skewness; however, for such a small sample, the data are not
unreasonably skewed. There are no outliers.
>x
63.4 65.0 64.4 63.3 54.8 64.5 60.8 49.1 51.0
mean(x) 59.58889
sd(x) 6.255287
sort(round(x))
49 51 55 61 63 63 64 64 65
stem(x)
The decimal point is 1 digit(s) to the right of the |
4
5
5
6
6
|
|
|
|
|
9
1
5
1334
55
to 63.47%. We are 90%
confident that the mean percent of nitrogen in ancient air is between
55.71% and 63.47%.
18.15 We prefer the t procedures to the z procedures for inference about a
population mean because
(a) z can be used only for large samples.
(b) z requires that you know the population standard deviation σ.
(c) z requires that you can regard your data as an SRS from the population.
Answer
(b) We virtually never know the value of σ.
18.19 You have an SRS of 12 observations from a Normally
distributed population. What critical value would you use to
obtain a 98% confidence interval for the mean μ of the
population?
(a) 2.718
(b) 2.681
(c) 2.650
Answer
(a) 2.718. Here, df = 11.
18.9 Is it significant? The one–sample t statistic from a sample of n = 15
observations for the two-sided test of
H0: μ = 64
Ha: μ 64
has the value t = 2.12.
(a) What are the degrees of freedom for t?
(b) Locate the two critical values t* from Table C that bracket t. What are the two-sided P–
values for these two entries?
(c) Is the value t = 2.12 statistically significant at the 10% level? At the 5% level?
(d) (Optional) If you have access to suitable technology, give the exact two-sided P–value for t =
2.12.
Answer
(a) df = 15 − 1 = 14.
(b) t = 2.12 is bracketed by t* = 1.761 (with two-tail probability 0.10) and
t* = 2.145 (with two-tail probability 0.05). Since this is a two-sided
significance test, 0.05 < P < 0.10.
(c) This test is significant at the 10% level since the P < 0.10. It is not
significant at the 5% level since the P > 0.05. (d) From software, P =
0.0524.
18.27 Reading scores in Atlanta. The Trial Urban District
Assessment (TUDA) is a government-sponsored study of student
achievement in large urban school districts. TUDA gives a
reading test scored from 0 to 500. A score of 243 is a “basic”
reading level and a score of 281 is “proficient.” Scores for a
random sample of 3000 eighth-graders in Atlanta had
with
13
standard error 1.0.
(a) We don’t have the 3000 individual scores, but use of the t
procedures is surely safe. Why?
(b) Give a 99% confidence interval for the mean score of all
Atlanta eighth-graders. (Be careful: the report gives the
standard error of
, not the standard deviation s.)
(c) Urban children often perform below the basic level. Is there
good evidence that the mean for all Atlanta eighth-graders is
less than the basic level?
Answer
(a) The sample size is very large, so the only potential hazard
is extreme skewness. Since scores range only from 0 to 500,
there is a limit to how skewed the distribution could be.
(b) From Table C, we take t* = 2.581 (df = 1000), or using
software take t* = 2.5775. For either value of t*, the 99%
confidence interval is 250 ± 2.581 = 247.4 to 252.6.
(c)
243
243
the
Because the 99% confidence interval for μ does not contain
and is entirely above 243, we would fail to reject H0: μ =
against the one-sided alternative hypothesis Ha: μ < 243 at
1% significance level.
# plots of Z and t
x <- seq(-4,4,length=100)
plot(x,dnorm(x),type="l",ylab="Density",xlab="Z, t")
lines(x,dt(x,df=10),lty=2,col=2)
legend(-4,max(dnorm(x)),c("Z","t
(df=10)"),lty=c(1,2),col=c(1,2),cex=.5)
set.seed(12345)
x <- rnorm(100, mean = 10)
# Use the t.test() function to compute a confidence interval
# for mu.x when the variance is unknown
t.test(x, conf.level = 0.95)$conf.int
# Of course, you could do it manually
mean(x)-qt(0.975,df=length(x)-1)*sqrt(var(x)/length(x))
mean(x)+qt(0.975,df=length(x)-1)*sqrt(var(x)/length(x))
set.seed(12345)
x <- rnorm(100, mean = 10)
y <- rnorm(100, mean = 5)
# Use the t.test() function to compute a confidence interval
# for mu.x - mu.y when the variances are unknown and unequal
t.test(x, y, conf.level = 0.95, var.equal = FALSE)
weather data text page 440:
20.8
18.7
19.9
20.6
21.9
23.4
22.8
24.9
22.2
20.3
24.9
22.3
27
20.4
22.2
24
21.1
22.1
22
22.7
Water quality data page 443:
160
40
2800
80
2000
2000
1500
400
150
500
3000
2200
15
80
2000
2000
2600
600
1000
1500
Chimpanzee data page 449:
16
16
23
19
15
20
24
24
0
1
5
3
4
9
16
20