* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Student t distribution
Survey
Document related concepts
Transcript
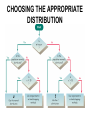
Section 7-4 Estimating a Population Mean: σ Not Known ASSUMPTIONS: σ NOT KNOWN 1. The sample is a simple random sample. 2. Either the sample is from a normally distributed population or n > 30. When σ is not known we will use the Student t Distribution. THE STUDENT t DISTRIBUTION If the distribution of a population is essentially normal, then the distribution of 𝑥−𝜇 𝑡= 𝑠 𝑛 is essentially a Student t distribution for all samples of size n, and is used to find critical values denoted by tα/2. The Student t distribution is often referred to as the t distribution. DEGREES OF FREEDOM Degrees of Freedom (df) corresponds to the number of sample values that can vary after certain restrictions have been imposed on all data values. In this section, degrees of freedom = n − 1 MARGIN OF ERROR ESTIMATE OF µ (WITH σ NOT KNOWN) 𝑠 𝐸 = 𝑡𝛼/2 ∙ 𝑛 where (1 − α) is the confidence level and tα/2 has n − 1 degrees of freedom. NOTE: The values for tα/2 are found in Table A3 which is found on page 606, inside the back cover, and on the Formulas and Tables card. CONFIDENCE INTERVAL ESTIMATE OF THE POPULATION MEAN μ (WITH σ NOT KNOWN) 𝑥−𝐸 <𝜇 <𝑥+𝐸 where 𝑠 𝐸 = 𝑡𝛼/2 ∙ 𝑛 CONSTRUCTING A CONFIDENCE INTERVAL FOR μ (σ NOT KNOWN) 1. 2. Verify that the required assumptions are met. Using n − 1 degrees of freedom, refer to Table A-3 and find the critical value tα/2 that corresponds to the desired confidence interval. (For the confidenc level, refer to “Area in Two Tails.”) 𝑠 𝑛 3. Evaluate the margin of error 𝐸 = 𝑡𝛼/2 ∙ 4. Find the values of 𝑥 − 𝐸 and 𝑥 + 𝐸. Substitute these in the general format of the confidence interval: 𝑥 − 𝐸 < 𝜇 < 𝑥 + 𝐸. Round the result using the same round-off rule from the last section. 5. FINDING A CONFIDENCE INTERVAL FOR µ WITH TI-83/84 1. 2. 3. 4. 5. 6. 7. 8. 9. Select STAT. Arrow right to TESTS. Select 8:TInterval…. Select input (Inpt) type: Data or Stats. (Most of the time we will use Stats.) Enter the sample mean, x. Enter the sample standard deviation, Sx. Enter the size of the sample, n. Enter the confidence level (C-Level). Arrow down to Calculate and press ENTER. PROPERTIES OF THE STUDENT t DISTRIBUTION 1. The Student t distribution is different for different sample sizes (see Figure below for the cases n = 3 and n = 12). PROPERTIES OF THE STUDENT t DISTRIBUTION (CONTINUED) 2. 3. 4. 5. The Student t distribution has the same general symmetric bell shape as the normal distribution but it reflects the greater variability (with wider distributions) that is expected with small samples. The Student t distribution has a mean of t = 0 (just as the standard normal distribution has a mean of z = 0). The standard deviation of the Student t distribution varies with the sample size and is greater than 1 (unlike the standard normal distribution, which has a σ = 1). As the sample size n gets larger, the Student t distribution gets closer to the normal distribution. CHOOSING THE APPROPRIATE DISTRIBUTION CHOOSING BETWEEN z AND t Method Conditions Use normal (z) distribution σ known and normally distributed population or σ known and n > 30 Use t distribution σ not known and normally distributed population or σ not known and n > 30 Population is not normally distributed and n ≤ 30. Use a nonparametric method or bootstrapping FINDING A POINT ESTIMATE AND E FROM A CONFIDENCE INTERVAL Point estimate of µ: upper confidence limit + lower confidence limit 𝑥= 2 Margin of error: upper confidence limit − lower confidence limit 𝐸= 2