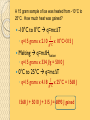Download Measurements - WordPress.com

Unit 9 Thermochemistry
Chapter 17
This tutorial is designed to help students
understand scientific measurements.
 Objectives for this unit appear on the next
slide.

◦ Each objective is linked to its description.
◦ Select the number at the front of the slide to go
directly to its description.

Throughout the tutorial, key words will be
defined.
◦ Select the word to see its definition.
Objectives
13 State the laws of thermodynamics
14 State the difference between temperature and heat
15 Identify variables and their labels for heat quantities
and solve thermochemistry problems
16 Calculate heat-lost heat-gained quantities
(calorimetry)
17 Interpret heating/cooling curves and identify the
phase changes.
13 The Laws of Thermochemistry
There are four laws of thermochemistry.
 The first three were written and then
another was added.

◦ The one that was added was thought to be
important enough that it should be listed first.
Zeroth Law of Thermodynamics

States that if two systems are at a thermal
equilibrium with a third, they are at a
thermal equilibrium with each other.
◦ Equilibrium occurs with there is no transfer of
heat from one system to another.
First Law of Thermodynamics

States that energy can be transformed
but it cannot be created or destroyed.
◦ This is sometimes known as the Law of
Conservation of Energy.
◦ Since heat is a type of energy, this law applies
to thermodynamics.
Second Law of Thermodynamics

States that heat always travels from hot to
cold.
◦ Heat cannot be transferred from a colder
object to a warmer object.
Third Law of Thermodynamics

States that absolute zero is the lowest
temperature and all molecular motion
stops at this point.
◦ Essentially, this means you cannot have a
temperature lower than 0 K.
Laws of Thermodynamics Recap
 0th
Law
◦ Thermal systems will form equilibrium
relationships when mixed.
 1st
Law
◦ Energy cannot be created or destroyed.
 2nd
Law
◦ Heat flows from hot to cold.
 3rd
Law
◦ All molecular motion stops at absolute zero.
14 Temperature vs. Heat
Temperature is often confused with heat but
the two are quite different.
Temperature is a measure of the average
kinetic energy of molecules.
Heat is the measure of the total kinetic energy
of molecules.
Temperature vs. Heat
All molecules are in a state of motion.
 The motion is measured by kinetic energy.
 However, not all molecules are moving at
the same speed and thus do not have the
same kinetic energy.
 The average is taken to determine the
speed of the majority of the molecules.
 The total is determined for a purpose
that will be discussed in Unit 9.

15 Heat Quantities
As discussed in Unit 10, temperature is
the average kinetic energy of molecules.
 Heat is the total kinetic energy of
molecules.
 Heat is measured in Joules or kiloJoules.
 To calculate heat, the following equation is
used:

q=mc∆T
Heat Quantities
q=mc∆T

For the equation above:
◦ Q = heat measured in joules
◦ m = mass of the object in grams
◦ c = specific heat of an object in
◦ ∆T = change in temperature
𝐽
𝑔°𝐶
Specific Heat
Every substance has a certain specific heat.
 This is the amount of heat required to raise the
temperature of one gram of an object by one
degree Celsius.
 Essentially, this number indicates how well on
object holds heat.

◦ The higher the amount, the longer it will take to heat.
 Consider water.
 It has a high specific heat. Therefore, a lake can be cool even on a
warm summer day. It takes the sun a long time to increase the
temperature of the water.
◦ The lower the value, the shorter it will take to heat.
 Consider a sandy beach.
 It has a low specific heat. Therefore, it heats up fast on a warm
summer day thus making it painful to walk on.
Heat Quantities
Since we have our equation, q=mc∆T, it is
possible to calculate missing variables.
 Consider:


These
amounts
are found
on the back
of the
Periodic
Table.
A copper wire gained 570 J of heat when its
temperature was increased from 25°C to 35°C. What
is the mass?
q = 570 J
m = ? Grams
c = 0.384
𝐽
𝑔°𝐶
q=mc∆T
570 J = X x 0.384
𝐽
𝑔°𝐶
x 10°C
∆T = 35°C - 25°C = 10°C
x = 150 grams
16 Heat Lost/Heat Gained

According to the laws of thermodynamics,
when two systems are placed together
they will form an equilibrium.

Therefore, heat will travel from the
warmer system to the colder system.

Because energy cannot be created or
destroyed, the heat lost by one system
equals that gained by the other system.
Calorimetry
A common use for the heat lost/heat
gained concept is calorimetry.
 Calorimetry is a technique used to
determine information about an unknown
object.
 It works by heating up an object and then
placing it into water. The temperature of
the water and the object will equilibrate
to the same temperature.

Calorimetry
1.
Heat object
2.
Place object in water
3.
Determine temperature
of system
Calorimetry
Consider:
An sample metal with mass of 931 grams was heated to
45°C and placed in 200 grams of water. The water
increased from 15°C to 25°C. What was the metal?
Sample
Water
931
200
0.449
4.18
Intial Temp. (°C)
45
15
Final Temp. (°C)
25
25
8360
8360
Mass (grams)
Specific Heat (J/g°C)
Heat (J)
Iron
Q=mc∆T
These numbers will be the same for each column
17 Heating Curves

As a substance gains heat, its molecules
will speed up.

Since molecules are speeding up, it is
possible for a phase change to occur.

During a phase change, the temperature
does not increase even though the heat
will.
Melting Point = 20°C
Boiling Point = 90°C
Vaporization/Condensation
Gas
Temperature (°C)
90
Melting/Freezing
Liquid
20
Solid
Heat (J)
Heating Curves and Heat Quantities
A problem occurs when calculating a heat
quantity when a phase change occurs.
 For instance, if ice is at 0°C and melts to a
liquid, it gained heat.

◦ However, using q=mc∆T would not work
because there was no ∆T.
Heat of Fusion/Heat of Vaporization


When a heat quantity needs to be calculated during a
phase change, the equation is modified.
Since each substance has a different specific heat for
each phase and the temperature does not change, these
variables are replaced.
◦ c∆T becomes ∆Hfusion for melting/freezing
◦ c∆T becomes ∆Hvaporization for
condensation/vaporization
q=mc∆T
q=m∆H
Heating Curves
On the slants use
q=mc∆T. On the flats
use q=m∆H
q=mc∆T
q=m∆Hvaporization
q=mc∆T
q=m∆Hfusion
q=mc∆T
Heating Curves

Consider:
◦ A 15 gram sample of ice was heated from
-10°C to 25°C. How much heat was gained?
This reaction undergoes a phase change at 0°C.
A 15 gram sample of ice was heated from -10°C to
25°C. How much heat was gained?

This this reaction touches three parts of
the curve, it will take three equations to
determine the heat gained.
◦ First, -10°C to 0°C  q=mc∆T
◦ Second, melting  q=m∆Hfusion
◦ Third, 0°C to 25°C  q=mc∆T

If these values are added together, we will
have the total heat gained.
A 15 gram sample of ice was heated from -10°C to
25°C. How much heat was gained?

-10°C to 0°C  q=mc∆T
◦ q=15 grams x 2.10

𝐽
𝑔°𝐶
x 10°C=315 J
Melting  q=m∆Hfusion
◦ q=15 grams x 334 J/g = 5010 J

0°C to 25°C  q=mc∆T
◦ q=15 grams x 4.18
𝐽
𝑔°𝐶
x 25°C = 1568 J
1568 J + 5010 J + 315 J = 6893 J gained
This concludes the tutorial on
measurements.
 To try some practice problems, click here.
 To return to the objective page, click
here.
 To exit the tutorial, hit escape.

Definitions-Select the word to return to the tutorial