* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Vocabulary - Hartland High School
Survey
Document related concepts
Transcript
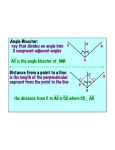
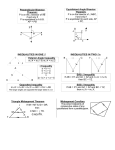
Section 5.3 Use Angle Bisectors of Triangles Goal Use angle bisectors to find distance relationships. TERM MEANING Angle Bisector Ray, line, or segment that divides an angle into two congruent adjacent angles PICTURE PS is the angle bisector of QPR The distance Distance from a point to a line Length of the perpendicular segment from the point to the line from S to PQ is SQ because SQ PQ O Incenter Concurrency of angle bisectors of a triangle QS = QR = QT R S Q N T ANGLE BISECTOR THEOREM If a point is on the bisector of an angle, then it is equidistant from the two sides of the angle. CONVERSE OF THE ANGLE BISECTOR THEOREM If a point is on the interior of an angle and is equidistant from the sides of the angle, then it lies on the bisector of the angle. If AD bisects BAC and DB AB and DB AC , If DB AB and DB AC and DB = DC, then Then DB = DC Example 1: Use the Angle Bisector Theorem a. Find the measure of CBE. AD bisects BAC b. Find the measure of LM . Example 2: Find the value of x that would make P lie on the bisector of J ? P Section 5.3 Use Angle Bisectors of Triangles Example 3: In the diagram, V is the incenter of ΔPQR. Find VS. Checkpoint 1. Find the value of x. 2. Find the value of x. 3. In the diagram, L is the incenter of ΔFGJ. Find LK.