Download Rotation and Centripetal Force

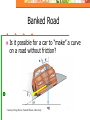
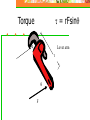
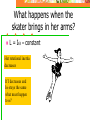
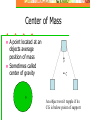
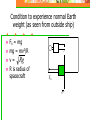
Coutesy Space.com
Rotation & Centripetal Force
How to Keep it Straight Without
Getting Dizzy
Rotation
In addition to side to side (linear)
motion, rotation plays an important role
in physics, engineering, and life.
 Name some common phenomena or
devices that show rotation

Tops, planets, bicycle, car wheels, gears, pulleys, fans
etc
Speed on a Wheel

Which horses on a
carousel move the
fastest, inner or
outer?
Outer
v = radius x angular
speed
v = rw
Way Cool Carousel Applet
Example

A person half way out from the center
of a rotating carousel walks all the way
to the edge. What happens to their
linear speed?
It doubles
Application of v = radius x
constant angular speed

Taper of train
wheels allows
wheels to have
different linear
speed on curve
although angular
speed is same fopr
each wheel
Mass at the End of a String
What force must the
string exert on the mass?
What is the direction of
this force?

A force toward the center of the
circle
Centripetal Force




Any force directed toward the center of a
circle is called centripetal.
Centripetal forces have clear causes such as
tension in a string, gravity, friction etc.
Some people call centripetal force a
“pseudoforce.” (not real)
They say “a real force such as friction
provides centripetal force.”
How Big is Centripetal Force?
Fc = mv2/r
 The faster the speed the more the force
 The tighter (smaller) the radius the
more the force
 v2/r is called centripetal acceleration

Is a mass moving at steady
speed in a circle accelerating?
Yes. The direction is changing
 What is the direction of this
acceleration?

Toward the center of the circle
Car on a Curve

When auto rounds corner, sideways
acting friction between tires and road
provides centripetal force that holds car
on road
Don’t Confuse Inertia With
Force


Tub’s inner wall exerts
centripetal force on
clothes, forcing them
into circular path
Water escapes through
holes because it tends
to move by inertia in a
straight line path
Clothes Washer
Photo courtesy HowStuffWorks.com
How Can Water Stay In The
Bucket?
Bucket swung in a
vertical circle
 What force pushes on the
water?

You have to swing the bucket fast enough
for the bucket to fall as fast as the water
There must be a “normal” force exerted by
the bottom of the bucket on the water, in
addition to gravity
Weight and
normal
force down
Centrifugal Force



The force ON THE
PAIL is inward
(centripetal)
The force ON THE
STRING is outward
(centrifugal)
If the string broke,
which way would
the can go?
Tangent to the circle
Change Your Point of View

In rest frame of the
can there appears to
be a centrifugal
force. This
pseudoforce(or
fictitious force) is a
result of rotation
Unlike real forces,
centrifugal force is not
part of an interaction
Book on a Car Seat
When a car goes around a curve to the
left, a book slides
 Which way does it slide?
 Why doesn’t it keep moving with the
car? There is not enough static friction force to keep it

going in a circle. This friction must provide the
necessary centripetal force.
The explanation in the rotating rest frame is different.
How?
Banked Road

Is it possible for a car to “make” a curve
on a road without friction?
Ff
Courtesy Doug Davis, Eastern Illinois University
A component of normal force (to the left) keeps the car moving
in a circle (provides centripetal force)
Rotating Space
Station from
“2001, A Space
Odyssey”
Torque
Produces rotation
 The rotational analog of force
 Depends on direction and where
applied
 Equals force times lever arm times sine
of angle between them t = rFsinq
 Unit is meter Newton
 Lever arm is perpendicular distance of
axis of rotation to line of action of force

t = rFsinq
Torque
Lever arm
r
Axis of
rotation
q
F
How to get the most torque
What angle gives the most torque?
 Where should you hold the wrench?

Balanced Torques
Net torque produces acceleration
 When torques are balanced we have
rotational equilibrium
 Torques act to rotate a system
clockwise or counterclockwise

Angular Momentum
Analog of linear momentum mv
 L = Iw (like mv in linear motion)
 I is rotational inertia or moment of
inertia, measuring how difficult it is to
rotate something
 Angular momentum is conserved

What happens when the
skater brings in her arms?

L = Iw = constant
Her rotational inertia
decreases
If I decreases and
Iw stays the same
what must happen
to w?
Center of Mass


A point located at an
objects average
position of mass
Sometimes called
center of gravity
An object won’t topple if its
CG is below point of support
CM of Moving Object
What would this look like if we threw the wrench
through the air?
Stable vs. Unstable Equilibrium


In stable equilibrium
a little rotation is
corrected (lowers
CG)
In unstable it leads
to toppling (raises
CG)
Neutral Equilibrium

In neutral
equilibrium the CG
does not get raised
or lowered
Challenge

Can you stand on tiptoes facing the wall
with toes against the wall for at least
several seconds?
Rotational Inertia

Why do tightrope walkers carry a long
pole?
Examples of Rotational Inertia
Simulated Gravity

The wall of the
space station applies
a centripetal force to
keep the person
moving in a circle.
In the rest frame of
the person this force
is centrifugal and is
experienced as
weight.
R
Condition to experience normal Earth
weight (as seen from outside ship)




Fn = mg
mg = mv2/R
v = Rg
R is radius of
spacecraft
Fn
mg