* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download 5.2 The Wave Equation
Identical particles wikipedia , lookup
Quantum electrodynamics wikipedia , lookup
Two-body Dirac equations wikipedia , lookup
Quantum state wikipedia , lookup
Perturbation theory (quantum mechanics) wikipedia , lookup
Perturbation theory wikipedia , lookup
Lattice Boltzmann methods wikipedia , lookup
History of quantum field theory wikipedia , lookup
Canonical quantization wikipedia , lookup
Interpretations of quantum mechanics wikipedia , lookup
Density matrix wikipedia , lookup
Bohr–Einstein debates wikipedia , lookup
Copenhagen interpretation wikipedia , lookup
Coherent states wikipedia , lookup
Hidden variable theory wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Molecular Hamiltonian wikipedia , lookup
Renormalization group wikipedia , lookup
Particle in a box wikipedia , lookup
Double-slit experiment wikipedia , lookup
Probability amplitude wikipedia , lookup
Path integral formulation wikipedia , lookup
Hydrogen atom wikipedia , lookup
Wave–particle duality wikipedia , lookup
Matter wave wikipedia , lookup
Wave function wikipedia , lookup
Erwin Schrödinger wikipedia , lookup
Dirac equation wikipedia , lookup
Schrödinger equation wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
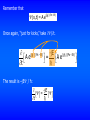
the wave equation Schrödinger’s Equation linearity and superposition expectation values “I think that I can safely say that nobody understands quantum mechanics.”—Richard Feynman (Nobel Prize, 1965) News Flash! Intel unveils silicon laser. News Flash! UMR Physics Professor uses laser to write quantum dots on the lightestweight material known to man. 5.2 The Wave Equation I have been claiming for several chapters now that particles have wave properties, and we have seen quite a few examples of experimental data that support this claim. Eventually, I am going to have to face the challenge, and come up with some serious mathematical theory to support this claim. If particles have wave properties and can be described by a wave function, there must be a wave equation for particles. I’m going to set out to find it. But one last time, let’s review the wave equation for waves. Here’s a “sophisticated” form of the wave equation: 2 y 1 2 y = 2 2 . 2 x v t The solution y(x,t) is a wave traveling with a speed v through space (one dimension) and time. (The above 1-dimensional equation can easily be generalized to 3 dimensions.) What are these things? They represent partial derivatives. If F is a function of (xyz), then when you take F/x, you treat y and z as constants: F If F(xyz) = 9xy + x yz , then = 9y 2 + 2xyz . x 2 2 Solutions to the wave equation have the form x y = Ft ± . v The - sign represents waves traveling in the +x direction, and the + sign represents waves traveling in the -x direction. An equivalent functional form is y = F ( k x t ) . An example of a solution of the wave equation is the wave equivalent to a free particle: y = A e j ( kx - ωt ) = A cos ( kx - ωt ) + j A sin ( kx - ωt ) . (A free particle is one which is not acted on by external forces, including those giving rise to a potential.) If we take the real part of y, we have the displacement of waves in a stretched string. (Beiser's equations are slightly different, but equivalent.) What have we accomplished in this section? Not much! We wrote down an “improved” form of the wave equation. We reminded ourselves that if objects are represented by waves, their wave functions must satisfy some form of a wave equation. 5.3 Schrödinger's Equation: Time-Dependent Form In this section we introduce Schrödinger's equation, which you can think of as a quantum mechanical statement of the conservation of energy, and which is probably the most important equation of quantum mechanics. Let's "derive" Schrödinger's equation. “Where did we get that from? It's not possible to derive it from anything you know. It came out of the mind of Schrödinger.”—Richard Feynman We begin with conservation of energy: 2 p E =K +U= +U, 2m where the potential U represents the effect of the rest of the universe on the particle (or system) we are studying.* U can represent the effect of applied electric fields, charged particles, gravity, springs, etc. Consider a particle (or system) represented by a wave function (x,t). *Do you see any relativity here? No, this is all nonrelativistic. There is a relativistic form for anybody who needs it. Multiply the energy conservation equation by (x,t) from the right: 1 (x,t) E = P2 (x,t) + U(x, t) (x,t) . 2m If this is to be a wave equation, it must have solutions of the form (x,t) = A e j (kx - ωt) =Ae (j/ ) (Px - Et) . The second part of the equation comes from E = ħ and P = ħk. I made the equation a bit bigger than normal so you could see the quantities in the exponents. (x,t) = A e j (kx - ωt) = A e(j/ ) (Px - Et) . Now, “just for kicks,” take 2/x2 A e(j/ x ) (Px - Et) = jP A e(j/ ) (Px - Et) The result is -P2/ ħ2 : 2 (j/ A e 2 x 2 jP ) (Px - Et) (j/ = A e ) (Px - Et) = - P2 2 (x, t) . 2 P2 = - 2 (xt) . 2 x Solving* for P2/2m, we get 2 P2 2 =. 2 2m 2m x *Why? Because it appears in our “energy conservation” expression. Remember that (x,t) = A e(j/ ) (Px - Et) Once again, “just for kicks,” take /t. A e(j/ t ) (Px - Et) = -jE The result is –jE / ħ: -jE = t A e(j/ ) (Px - Et) Solving* for E, we get E = j . t Plugging what we have found for E and P2/2m back into our “conservation of energy” equation gives 2 2 j =+U . 2 t 2m x This is the one-dimensional form of the time-dependent Schrödinger equation; it is easy to generalize to 3 dimensions. Although this equation represents the foundation of quantum mechanics, I won’t make it “official.” I’ll save that for a later version. *Why? Because it appears in our “energy conservation” expression. “Thus the partial differential equation entered theoretical physics as a handmaid, but has gradually become mistress.”—A. Einstein Our original equation 1 2 E (x, t) = p (x, t) + U(x, t) (x, t) 2m was deceptive, because p really represents the operator /x (remember, in Newtonian mechanics momentum is related to velocity, which is the first derivative of position) and E represents the operator /t. Our simple “conservation of energy” equation was really a linear differential equation. We have “justified” Schrödinger's equation, but not derived it. That’s OK—we never derive Newton’s laws either. We justify them, show that they work, and use them. We believe them because they describe reality. The same holds for Schrödinger's equation. It is a postulated first principle, arrived at by observation of physical reality, and believed in because it successfully describes the universe. In other words, we believe it because it works.* 2 Ψ 2 j =+U . 2 t 2m x Schrödinger's equation is a linear differential equation for the wavefunction . The potential U(x,t), may simply be zero or a numerical constant, or it may be a complicated operator. U(x,t) represents the effects of the universe on the particle. *That’s a sign of strength, not weakness. Schrödinger’s equation has been used to explain the previously unexplainable and predict the previously unthought. If you want to replace Schrödinger’s equation with something else, the “something else” must do everything Schrödinger’s equation does, and more. 2 Ψ 2 j =+U . 2 t 2m x Once we know some boundary conditions for the particle and the potential U(x,t), in principle we can solve for the wave function at any time t and position x. Once we have the wave function, our problem is “solved.” In this chapter we will solve Schrödinger's equation for some simple potentials. Let’s get to work… But before that, just to whet your appetite, this is what we are leading up to… from http://www.nearingzero.net What’s the simplest potential you can think of? That’s right: U=0, which is the potential for a free particle. We could take Schrödinger's equation, plug in U=0, and solve for . Or we could be “efficient*” and take our free-particle , plug it into Schrödinger's equation, and see if we come up with an identity. Let’s try that. *Lazy? The free-particle wave function is = e-(j/ ) (Et - Px) . The free-particle Schrödinger equation (U = 0) is 2 Ψ 2Ψ j =. 2 t 2m x Left-hand side: j e-(j/ ) (Et - Px) t =- j jE e-(j/ ) (Et - Px) =E . Right-hand side: - 2 2m 2 e-(j/ ) (Et - Px) x 2 =- 2 -jP 2m 2 -(j/ e 2 P ) (Et - Px) = 2m . P2 Setting LHS = RHS: E = . 2m P2 E = . 2m Remember—I told you this is the nonrelativistic version. Duh. We already knew that. Of course! But we needed to check for consistency in the simplest case before spending any more time on Schrödinger's equation. What can we do that’s useful? Patience! There are still a few ideas to introduce. 5.4 Linearity and Superposition In quantum mechanics, the physics and the math seem to be forever entangled. That means we can often gain insight by looking at the math, independent of a particular physical system. It also means that wave functions “behave well.” 2 2 j =+U 2 t 2m x Schrödinger's equation is linear in . In other words, it has no terms independent of , and no terms involving higher powers of or its derivatives. As a consequence of this linearity, if 1 and 2 are solutions to Schrödinger's equation, then so is the linear combination = a11 + a2 2 , where a1 and a2 are constants. A further consequence of this is that wave functions obey superposition and exhibit interference. (Duh, they represent waves, so they had better do these things, and all other things wavelike.) If a system is represented by a wave function = a11 + a22, how do we calculate the probability density for ? You can’t just add probabilities! You can’t write P = a1P1 + a2P2, where P1 = 1* 1 and P2 = 2*2! Instead, P = * = a 1 1 + a2 2 a 1 1 + a2 2 * a + a a + a a + a a + a a P = a1* 1* + a*2 *2 P = a1* 1* 1 1 * 1 1 1 * 1 2 2 2 * 2 2 * 2 1 1 * 2 * 2 2 P = P1 +P1 + a*2 *2 a 1 1 + a*2 *2 a2 2 Interference terms! Waves interfere! Beiser uses this result to show why electrons “shot” through a double slit exhibit interference effects (unlike “pure particles” but like waves). Be sure to read section 5.4! 2 5.5 Expectation Values Once we solve Schrödinger's equation for , we know all about the particle that is knowable within the limits imposed by the uncertainty principle. I've already told you how to calculate the probability of finding the particle in some volume element centered on the coordinates (x,t) in one dimension or (x,y,z,t) in three dimensions. P(x1 x x 2 ) = x2 x1 r2 * dx P(r1 r r2 ) = * dV . r1 Sometimes we want to calculate the average value of some measurable quantity. Just as quantum mechanics has its own way of calculating probabilities, quantum mechanics has its own special way of calculating averages. Let's begin with an example. Suppose we want to find the average of the set of numbers 1,1,1,2,2,3,3,3,3,4,4,4,4,4. How do you calculate the average? Add the numbers up and divide by the number of numbers? That works, but what if we have zillions of numbers. Is there a way to be clever? The average is 3×1 + 2 ×2 + 4 ×3 + 5 ×4 . 3 + 2 + 4 +5 In general, the average of Ni numbers having values xi is N x x= N i i i i . i If the variable x is continuous, you replace the sums by integrals. In quantum mechanics, the probability Pi of finding a particle in an interval dx at xi is 2 Pi dx = i dx . Think of * as being “like” N (“how much probability” “how many”). To get QM average <x>… N x x= N i i i i . i …replace this by *… …replace this by * with an extra x in it… …and replace these by integrals (because our variables are continuous). In QM (quantum mechanics) because we are dealing with probabilities, we use the term “expectation value” rather than “average value.” The expectation value of x is x = x * dx - - * dx “like” N , where we have replaced a discrete variable by a continuous one and let the sums become integrals. The expectation value is the quantum mechanical equivalent of an average value. If is normalized, the integral in the denominator equals one, and x = x * dx . - This is not “official” yet, because there is still a problem. Position, momentum, energy, kinetic energy, etc. are actually operators, and the order in which we take them is important. Remember, momentum is related to /x and energy is related to /t. The correct approach is to make a “* sandwich” to get an expectation value. x = * x dx - In general, the expectation value of any quantity, including operators, is G x = *G x dx . - Using the operator expression for momentum also prevents us from using the “hat” reminds us pˆ = pˆ dx * momentum is an operator - to claim we’ve found a way to violate the uncertainty principle. Let's use our wave function (x) = 3 x for 0 x 1 as an example. Refreshing your memory… The expectation value of x is like the average probability of finding a particle at coordinate x. It is the point where you could “balance” the * plot on your fingertips. I am going to move the laser pointer along the x-axis. You say “stop” when you think I reached the point where the red shaded area would balance on my fingertip. Now let’s see if the math agrees with you. x = x dx = - * 1 0 3x x 4 1 x 3 x dx = 3 x dx = 3 0 4 1 3 3 = . 4 0