* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Chapter 9: Introduction to the t statistic
Psychometrics wikipedia , lookup
History of statistics wikipedia , lookup
Foundations of statistics wikipedia , lookup
Degrees of freedom (statistics) wikipedia , lookup
Sufficient statistic wikipedia , lookup
Confidence interval wikipedia , lookup
Bootstrapping (statistics) wikipedia , lookup
Taylor's law wikipedia , lookup
Misuse of statistics wikipedia , lookup
Chapter 9: Introduction to
the t statistic
The t Statistic
• The t statistic allows researchers to use sample
data to test hypotheses about an unknown
population mean.
• The particular advantage of the t statistic is that
the t statistic does not require any knowledge of
the population standard deviation, i.e. σ.
• When σ is unknown, we cannot use z score to
test the hypothesis, but we can use t statistic
instead.
The t Statistic (cont’d.)
• Thus, the t statistic can be used to test
hypotheses about a completely unknown
population; that is, both μ and σ are unknown,
and the only available information about the
population comes from the sample.
• All that is required for a hypothesis test with t is
a sample and a reasonable hypothesis about the
population mean.
The Estimated Standard Error and the t
Statistic
• The goal for a hypothesis test is to evaluate the
significance of the observed discrepancy
between a sample mean and the population
mean. (M – μ)
• Whenever a sample is obtained from a
population you expect to find some discrepancy
or "error" between the sample mean and the
population mean.
• This general phenomenon is known as
sampling error.
The Estimated Standard Error and the t
Statistic (cont’d.)
• The hypothesis test attempts to decide between
the following two alternatives:
1. Is it reasonable that the discrepancy between M
and μ is simply due to sampling error and not
the result of a treatment effect?
2. Is the discrepancy between M and μ more than
would be expected by sampling error alone?
That is, is the sample mean significantly
different from the population mean?
The Estimated Standard Error and the t
Statistic (cont.)
• The critical first step for the t statistic hypothesis
test is to calculate exactly how much difference
between M and μ is reasonable to expect.
• However, because the population standard
deviation is unknown, it is impossible to compute
the standard error of M as we did with z-scores
in Chapter 8.
• Therefore, the t statistic requires that you use
the sample data to compute an estimated
standard error of M. i.e. sM
The Estimated Standard Error and the t
Statistic (cont’d.)
• This calculation defines standard error exactly
as it was defined in Chapters 7 and 8, but now
we must use the sample variance, s2, in place of
the unknown population variance, σ2 (or use
sample standard deviation, s, in place of the
unknown population standard deviation, σ).
• The resulting formula for estimated standard
error is:
s2
s
sM = ──
or
sM = ──
n
n
The Estimated Standard Error and the t
Statistic (cont’d.)
• The t statistic (like the z-score) forms a ratio.
• The top of the ratio contains the obtained
difference between the sample mean and the
hypothesized population mean.
• The bottom of the ratio is the standard error
which measures how much difference is
expected by chance.
obtained difference
Mμ
t = ───────────── = ─────
standard error
sM
The Estimated Standard Error and the t
Statistic (cont’d.)
• A large value for t (a large ratio) indicates that
the obtained difference between the data and
the hypothesis is greater than would be
expected if the treatment has no effect.
• For a small sample and unknown σ:
• t ↑ more likely to be effective, more likely to
reject H0
Degrees of Freedom
• Degrees of freedom is the number of values
which are involved in the final calculation of a
statistic that is expected to vary, or free to vary.
• In other words, these are the independent part
of data used in calculation. It is used to know the
accuracy of the sample population used in
research. The larger the degree of freedom,
larger the possibility of the entire population to
be sampled accurately.
Degrees of Freedom and the t Statistic
• You can think of the t statistic as an "estimated
z-score."
• The estimation comes from the fact that we are
using the sample variance s to estimate the
unknown population variance σ.
• With a large sample, the estimation is very good
and the t statistic will be very similar to a zscore.
• With small samples, however, the t statistic will
provide a relatively poor estimate of z.
Degrees of Freedom and the t Distribution
• The value of degrees of freedom, df = n - 1, is
used to describe how well the t statistic
represents a z-score.
• Also, the value of df will determine how well the
distribution of t approximates a normal
distribution.
• For large values of df, the t distribution will be
nearly normal, but with small values for df, the t
distribution will be flatter and more spread out
than a normal distribution.
• df ↑ , then t ~ Normal
z vs t
• σ : the same for every sample
z
M M-μ : varies
n
• s : varies for different sample
M
t
s
n
M-μ : varies
s : varies
Using the t-Distribution: σ Unknown
It is, like the z distribution, a continuous distribution.
It is, like the z distribution, bell-shaped and symmetrical.
There is not one t distribution, but rather a family of t distributions.
All t distributions have a mean of 0, but their standard deviations
differ according to the sample size, n.
The t distribution is more spread out and flatter at the center than
the standard normal distribution As the sample size n increases,
however, the t distribution approaches the standard normal
distribution.
Comparing the z and t Distributions When n is
Small, 95% Confidence Level, n = 5
William Sealy Gosset
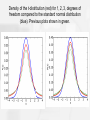
Density of the t-distribution (red) for 1, 2, 3, degrees of
freedom compared to the standard normal distribution
(blue). Previous plots shown in green.
Using the Student’s t-Distribution Table
p. 290
2. a. s
2
b. sM
SS
n 1
S
n
= 288/8 = 36
63 2
4. df = n-1 = 20 n = 21
5. df = 15, check p. 703
a. top 5% t = 1.753
b. middle 95% t = 2.131
c. middle 99% t = 2.947
Hypothesis Setups for Testing a Mean
()
10-*
Degrees of Freedom and the t Distribution
(cont’d.)
• To evaluate the t statistic from a hypothesis test, 1.select
an α level, 2.find the value of df for the t statistic, and
3.consult the t distribution table.
– If the obtained t statistic is larger than the critical
value from the table, you can reject the null
hypothesis.
– In this case, you have demonstrated that the obtained
difference between the data and the hypothesis
(numerator of the ratio) is significantly larger than the
difference that would be expected if there was no
treatment effect (the standard error in the
denominator, the “random error”).
Hypothesis Tests with the t Statistic
• The hypothesis test with a t statistic follows the
same four-step procedure that was used with zscore tests:
1. State the hypotheses and select a value for α.
(Note: The null hypothesis always states a
specific value for μ.)
2. Locate the critical region. (Note: You must find
the value for df and use the t distribution table.)
3. Calculate the test statistic. t statistic
4. Make a decision. (Either "reject" or "fail to
reject" the null hypothesis.)
Example 9.1 (p. 292)
n = 9, M = 13, SS = 72 : unknown population
1. H0: μ = 10 seconds (no preference/indifferent)
H1: μ ≠ 10 seconds (not indifferent)
α = 0.05
2. df = n-1 = 8
critical region: |t| > 2.306
3. s2 = SS/df = 72/8 = 9 s = 3 sM = s/√n = 1
t = (M- μ)/sM = 3 > 2.306
4. reject H0, i.e. it is more likely that μ ≠ 10
• Infants do prefer an attractive face, why?
Hypothesis Tests with the t Statistic
(cont’d.)
• There are two general situations where this type
of hypothesis test is used:
1. To determine the effect of treatment on a
population mean μ
2. In situations where the population mean μ is
unknown
Hypothesis Tests with the t Statistic
(cont’d.): case 1 (before/after)
1. In order to determine the effect of treatment on
a population mean, you must know the value of
μ for the original, untreated population. A
sample is obtained from the population and the
treatment is administered to the sample. If the
resulting sample mean is significantly different
from the original population mean, you can
conclude that the treatment has a significant
effect.
Hypothesis Tests with the t Statistic
(cont’d.): case 2 (theory/logic/guess)
2. Occasionally a theory or other prediction will
provide a hypothesized value for an unknown
population mean. A sample is then obtained
from the population and the t statistic is used to
compare the actual sample mean with the
hypothesized population mean. A significant
difference indicates that the hypothesized value
for μ should be rejected.
Hypothesis Tests with the t Statistic
(cont’d.): Assumptions
• Two basic assumptions are necessary for
hypothesis tests with the t statistic:
– The values in the sample must consist of
independent observations. (random sample, iid)
– The population that is sampled must be normal.
Hypothesis Tests with the t Statistic (cont’d.)
• Both the sample size n and the sample variance
s influence the outcome of a hypothesis test.
• The sample size is inversely related to the
estimated standard error. Therefore, a large
sample size increases the likelihood of a
significant test. n↑ sM ↓ t ↑
• The sample variance, on the other hand, is
directly related to the estimated standard error.
Therefore, a large variance decreases the
likelihood of a significant test. s↑ sM ↑ t ↓
p. 295
• μ = 40, n = 4, after treatment: M = 44, s2 = 16
a. two-tailed, α = 0.05, significant?
sM = 4/2 = 2, df = 3, critical region: |t|>3.182
t = (44-40)/2 = 2 < 3.182 failed to reject H0
no significant effect after treatment
b. n = 16, other things being equal, significant?
sM = 4/4 = 1, df = 15, critical region: |t|>2.131
t = (44-40)/1 = 4 > 2.131 reject H0
does have a significant effect
Measuring Effect Size for the t Statistic
• Because the significance of a treatment effect is
determined partially by the size of the effect and
partially by the size of the sample, you cannot
assume that a significant effect is also a large
effect.
• Therefore, it is recommended that a measure of
effect size be computed along with the
hypothesis test.
Measuring Effect Size for the t Statistic
(cont’d.)
• For the t test, it is possible to compute an
estimate of Cohen’s d just as we did for the zscore test in Chapter 8. The only change is that
we now use the sample standard deviation
instead of the population value (which is
unknown).
mean difference
M μ
estimated Cohen’s d = ─────────── = ──────
standard deviation
s
Example 9.2 (p. 296)
n = 9, M = 13, SS = 72 : unknown population
H0: μ = 10 (indifferent)
s2 = SS/df = 72/8 = 9 s = 3
Cohen’s d = (M- μ)/s = (13-10)/3 = 1
the size of treatment effect is equivalent to 1
standard deviation (shift to the right from μ = 10)
Measuring Effect Size for the t Statistic
(cont’d.)
• As before, Cohen’s d measures the size of the
treatment effect in terms of the standard
deviation.
• With a t test, it is also possible to measure effect
size by computing the percentage of variance
accounted for by the treatment.
• This measure is based on the idea that the
treatment causes the scores to change, which
contributes to the observed variability in the
data.
Measuring the percentage of variance
explained
• r2 = variability accounted for (by treatment effect) / total
variability = (SS1-SS2)/SS1
SS1:deviation from the hypothesized μ = total deviation =
Σ(X-μ)2
SS2: deviation from the hypothesized μ after removing the
treatment effect = Σ(X-M)2
• deviation caused by the treatment = variability accounted
for (by treatment effect) = (SS1-SS2)
• treatment removed from each score: (M-μ )
SS2 {[ X (M )] }2 ( X M )2 ( X M )2
Measuring the percentage of variance explained
• indifferent: μ = 10, but M = 13, ∆= M - μ = 3
• How much of the variability is explained by
treatment effect?
(a) SS1 = Σ(X-μ)2 = 153 :total variability from μ
(b) SS2 = Σ(X-M)2 = 72 :adjusted variability from μ
(treatment effect removed, i.e. remove the ∆ )
variability accounted for = SS1 - SS2 = 81
r
2
2
2
(
X
)
(
X
M
)
2
(
X
)
SS1 SS2
SS1
SS2 {[ X (M )] }2 ( X M )2 ( X M )2
Percentage of variance accounted for by treatment
2
•
r2
vs
t2
:
t
r 2
t df
2
SS1 ( X )2 [( X M ) (M )]2 ( X M )2 n(M )2
SS1 SS 2 ( X M ) 2 n( M ) 2 ( X M ) 2
n( M ) 2
r
2
2
SS1
( X M ) n( M )
( X M ) 2 n( M ) 2
2
(M )2
n df ( M ) 2
t
2
( X M ) n df
( X M ) 2
2
t2
n( M ) 2
2
t df ( X M ) 2 n(M ) 2
Measuring Effect Size for the t
Statistic (cont’d.)
• By measuring the amount of variability that can
be attributed to the treatment, we obtain a
measure of the size of the treatment effect. For
the t statistic hypothesis test:
percentage of variance accounted for = r2
t2
= ─────
t2 + df
Cohen’s d and r2
•
•
•
•
d : not influenced by n
d : will be affected by s
s↑ d↓
r2 : only slightly affected by n
•
•
•
•
Interpreting r2 : (proposed by Cohen)
r2 = 0.01 small effect
r2 = 0.09 medium effect
r2 = 0.25 large effect
Measuring Effect Size for the t
Statistic (cont’d.)
• The size of a treatment effect can also be
described by computing an estimate of the
unknown population mean after treatment.
• A confidence interval is a range of values that
estimates the unknown population mean by
estimating the t value.
• A confidence interval is also an interval
estimate of the population mean.
• A 95% confidence interval means 95% of
“confidence” that μ is in that interval.
Measuring Effect Size for the t
Statistic (cont’d.)
• The first step is to select a level of confidence
and look up the corresponding t values in the t
distribution table.
• This value, along with M and sM obtained from
the sample data, will be plugged into the
estimation formula:
μ = M ± tsM
M
t
sM
M t sM
Example 9.3 (p. 301)
• n = 9, df = 8, M = 13, SM = 1, check t table:
80% confidence interval, t = 1.397 13 1.397 *1
80% confidence interval = (11.603, 14.397)
90% confidence interval, t = 1.86 13 1.86 *1
95% confidence interval, t = 2.306 13 2.306 *1
99% confidence interval, t = 3.355 13 3.355 *1
• We assume that the t distribution is exactly what
we’ve constructed, so 80% of the probability that
true population mean is in this interval.
Confidence Interval
• confidence level ↑ interval width ↑
• n ↑ sM ↓ interval width ↓
i.e. n ↑ more info more precise estimate
M
t
sM
M t sM
Report about your test result
• p. 302-303:
provide info about sample statistics and test
statistics and test result/interpretation, eg. M, n,
s, t, p, r2 , confidence interval etc.
• report an exact p value if you can, otherwise
report p < , or p > etc.
p. 303
1. n=16, μ=80, M = 86, s=8, α=0.05 sM =8/4=2
a. two-tailed test, significant?
df = 15, critical t = 2.131
t = 6/2=3 > 2.131 significant
b. Cohen’s d and r2 = ?
d = (M- μ)/s=6/8 = 0.75
r2 = 9/(9+15)=0.375
c. 95% CI=?
86 2.131*2 = (81.738, 90.262)
2. n↑ sM ↓ t↑ more likely to reject H0 , but no effect
on effect size d
s ↑ sM ↑ t↓ less likely to reject H0 , effect size d ↓
Directional / One-tailed test
Example 9.4 (p. 304) infant preference
M = 13, n = 9, SS = 72 sM = 3/3 = 1
H1: μ>10, α = 0.01
df = 8, critical region: t > 2.896
test statistic t = (13-10)/1 = 3 > 2.896
reject H0 infant spend significantly more
time looking at the attractive face
• Note: one-tailed test has a larger rejection
region more likely to reject H0 than twotailed test with the same α
p. 306
normal: μ = 200, n = 9, M = 206, SS = 648, α=0.05
a. H1: μ ≠ 200 critical t = 2.306
s = 648/8 = 81, sM = 9/3 = 3
t = 6/3 = 2 < 2.306 failed to reject H0
b. t(8) = 2, p > 0.05 no significant effect
c. H1: μ > 200 critical t = 1.86
t = 6/3 = 2 >1.86 reject H0
d. t(8) = 2, p > 0.05 significantly increases the
reaction time