* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Matter and Measurement Ppt.
Elementary particle wikipedia , lookup
Abundance of the chemical elements wikipedia , lookup
Chemistry: A Volatile History wikipedia , lookup
History of molecular theory wikipedia , lookup
Crystallization wikipedia , lookup
Gas chromatography wikipedia , lookup
Analytical chemistry wikipedia , lookup
Registration, Evaluation, Authorisation and Restriction of Chemicals wikipedia , lookup
History of chemistry wikipedia , lookup
Particle-size distribution wikipedia , lookup
Vapor–liquid equilibrium wikipedia , lookup
Dimensional analysis wikipedia , lookup
Condensed matter physics wikipedia , lookup
Gas chromatography–mass spectrometry wikipedia , lookup
Size-exclusion chromatography wikipedia , lookup
Thermomechanical analysis wikipedia , lookup
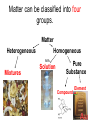
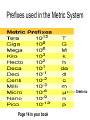
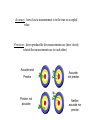
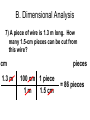
Honors Chemistry Chapter 1 Matter and Measurement 1.1 What is chemistry? • Chemistry is the study of the properties of matter and their changes. • Matter: The physical material of the universe. – Anything that has mass and – Occupies space (volume) Matter • Matter: Anything that has mass and takes up volume • Mass: the amount of material (stuff) in an object (kg, g, lb, t ) • Volume: the amount of space an object occupies (cm3, mL, L, ci) Elements • Very basic elementary substances. • Made of unique atoms. • Can not be broken down further without changing the identity. • Named for Latin or Greek characters or places. • Represented by 1 or 2 letter symbols. – First letter CAPITALIZED – Second letter lower case • C, O, Co • CO vs. Co Hydrargyrum Greek for “liquid silver” Molecules • Combinations of two or more atoms held together in specific shapes. • Properties are based on the structure and arrangement , and the number and types of atoms present. Methane Classifications of Matter • • • How is matter classified? (2 ways) 1. Macroscopic level (more than one molecule) a. Gas or vapor (g): no volume or shape, highly compressible • • • gases expands to occupy it’s container. b. Liquid (l): volume independent of container, no shape, incompressible (relatively) c. Solid (s): volume and shape independent of container, rigid, incompressible. 2. Molecular level (single molecules) • a. gas: • b. liquid: molecules closer than gas, move rapidly, slide over each other • c. solid: molecules packed closely, definite arrangement, don’t move. molecules far apart, high speed, collide often with each other, and container walls. (kinetic molecular [KM] theory) States of matter (4) • 1. Solids • Hold a particular shape. • Have a definite volume. • Particles arranged in an orderly manner. • High density States of Matter • 2. Liquid • Does not hold its own shape, takes the shape of its container. • Has definite volume. • Particles arranged randomly • High density • Not compressible States of Matter • 3. Gas • No definite shape or volume. • Expands to occupy the space of its container. • Extremely low density. • Particles far apart. • Highly compressible. • Density depends on pressure. – High pressure forces particles closer. States of Matter • 4. Plasma • Ionized gasses. • Ions and electrons (charged particles) • Found in the center of stars and space. • Emit light when “excited” • Eg. Lightning, Northern Lignts Matter Matter can be classified into four groups. Heterogeneous Matter Homogeneous AKA: Solution Mixtures Pure Substance Compound Element Pure Substances (2 types) 1. Pure substance is a substance with constant composition 2. Pure substances have fixed measurable properties 3. Pure substances cannot be found in nature. C6H12O6 H 2O Elements (pure substance #1) 1. Simplest form of matter. 2. Can not be broken down by ordinary chemical means. 3. 92 naturally occurring elements.(118 total) 4. Arranged in the periodic table. 5. Solids, Liquids, Gases (at room temp) Symbol Atomic Number Mass Number http://www.funbrain.com/periodic/ (Atomic Weight) Element names and symbols to memorize. (on periodic table) 2A Be Mg Ca Sr Ba 3A B Al 4A C Si Sn Pb 5A N P 6A O S 7A F Cl Br I 8A He Ne Ar Kr Rn K R b 1A H Li Na K Rb Transition Metals to Memorize • • • • • • • • • • Cr Mn Fe Co Ni Cu Zn Ag Hg Au • • • • • • • • Diatomic Elements H2 N2 O2 F2 Cl2 Br2 I2 • BrINClHOF Compounds (pure substance #2) Two or more elements combined in a chemical reaction. • Elements are in fixed proportions to each other. • Written using symbols with subscripts to denote the ratio of elements. • Can not be separated by physical means. H2O: 2 Hydrogen: 1 Oxygen Mixtures • A combination of two or more pure substances. • Two types of mixtures. Heterogeneous mixture (hetero: different) • A MIXTURE is a combination of – two or more pure substances that are – not chemically united and – do not exist in fixed proportions to each other. – Do not have uniform composition. • Most natural substances are mixtures. • A heterogeneous mixture consists of visibly different substances or phases. • A mixture can be physically separated into pure compounds or elements. Methods of separating mixtures • 1. Decantation: pouring a less dense liquid off the top of a more dense liquid. • 2. Filtration: Separating particles based on size or phase. Larger particles are trapped in the filter. • Liquid passes through filter, solid is trapped. Separating Funnel Homogeneous Mixture (Homo: Same) Solution • A homogeneous mixture has the same uniform appearance and composition throughout. Many homogeneous mixtures are commonly referred to as solutions. • All components are all in the same phase. • Particles are uniform in size (atoms or molecules) • Can not be separated by physical means. • Can be separated based on differences in properties of components. Methods of separating solutions • 3. Crystallization: Evaporating one component to leave another. • 4. Chromatography: Separating components based on specific gravity. • 5. Distillation: Separation of liquids based on differences in boiling point. Properties of compounds vs. elements. • A compound may have different properties than the elements composing it. • Hydrogen H2: Gas • Oxygen O2: Gas • Water H2O: Liquid Joseph Proust (1799) • French Chemist • Developed The Law of Definite Proportions • Aka the Law of Constant Composition • Compounds always contain the same elements in the same proportion by mass. Law of Definite Proportions • H20 (by mass is always) • 88.9% Oxygen, 11.1% Hydrogen • If we had an 80g sample of H20 how much is O? • .889 x 80 = 71g • How much is H? • .111 x 80 = 9g 1.2 Properties of Matter • Physical Properties: • Characteristics that can be observed and measured without altering the identity of the substance. • Density, color, melting point, odor, boiling point, etc. Ice, water and steam. Physical Properties: 2 Types • 1:Intensive Properties: • Do not depend on the amount of matter present. • Examples: – – – – – – Density Conductivity Melting point Boiling point Temperature Pressure Physical Properties: 2 Types • 2: Extensive Properties • Depends on how much material is on hand. • Changes with the amount of material present. • Examples: – Mass – Volume – Weight Chemical Properties • The way matter behaves when brought into contact with other substances, or a source of energy. • Describes how substances react with other substances. • Example: – Flammability – Inert (nonreactive) “Oh the humanity” Changes in Matter • Physical Changes: • Alter the form, but do not alter the identity of the substance. • Change in physical appearance. • Examples: – Crushing – Tearing – Changes of state (phase) Chemical Changes (Reactions) • Chemical Changes (reactions) • Changes a substance into chemically different substances. • Irreversible • Alters the identity of the substance being changed. • Examples: – Wood burning, – Food cooking, – Iron rusting Homework Practice • Exercises #s 2, 3, 5, 10, 12, 15 • On page 29 in Textbook 1.4 Units of Measurement & the Metric System A. Why Measure? In order to get complete observations, quantifying is essential. B. Consists of: 1. 2. C. Quantity a. Anything that can be measured b. Involves a number followed by a unit c. Examples: Volume, Mass, Length, Time Unit (can be English (customary) or metric) a. Is what unit the quantity is measured in b. Examples: Liter, Gallon, Gram, Foot, Meter, Second Why Use the Metric System? 1. It’s easier because it is based on units of 10 2. Everyone uses it so it gives consistency 3. There are standards that everyone can compare to D. International System of Units – called SI 1. Composed of fundamental or base units. Chart 1-1 Quantity Standard Unit Symbol Length Meter m Mass Kilogram kg Time Second s Amount/Count Mole mol or m (bar) Temperature Kelvin K Electric Current Ampere A Luminous Intensity Candela cd Prefixes used in the Metric System Greek mu Page 14 in your book Length and Mass • SI unit of length is the meter (m) (ca. 39 inches) • Mass: The measure of the amount of material (matter, stuff) in an object. • SI base unit of mass is the kilogram (kg) (ca. 2.2 lbs) • This is odd because it uses a prefix instead of gram alone. Temperature • The measure of how fast molecules in a substance are moving. » Or • The measure of the average kinetic energy of particles in a substance. Temperature scales • Fahrenheit • Named after Gabriel Fahrenheit (1686-1736) • Thermometer maker who devised his own temperature scale. • Based on the temperature of an equal ice-salt mixture. (0ºF) • Average temperature of a healthy horse. (100 º F) • H2O freezes at: 32º F • H20 boils at 212º F Why me? Say aaah. Temperature Scales • Celsius (Centigrade) • Anders Celsius • Developed a temperature scale more compatible with the metric system. • Based on H20 – H2O freezes at: 0º C – H20 boils at 100º C (1701- 1744) Thanks Mr. Celsius!! Fahrenheit vs Celsius • Fahrenheit – 212º - 32º = 180º from boiling to freezing. • Celsius – 100º - 0º = 100º from boiling to freezing. • 180/100 = 9/5 • Celsius degrees are 9/5 bigger than Fahrenheit • The Fahrenheit scale also begins 32º above the Celsius scale. Converting between Fahrenheit and Celsius • Taking the degree size, and starting point in consideration, we get: • ºF = 9/5ºC + 32 and/ or • ºC = 5/9(ºF – 32) *watch order of ops* Conversion Practice • The temperature of a healthy human is 98.6ºF. Convert this to Celsius. • ºC = 5/9 (98.6ºF – 32) • 37ºC • A baby has a fever of 39.5ºC. What is her temperature in Fahrenheit? • ºF = 9/5 x 39.5ºC + 32 • 103.1 ºF The Kelvin Temperature Scale • The SI unit used to measure temperature. • Named for William Thomson, Lord Kelvin • Not Melvin Kelvin • The º symbol is not used for kelvin (K) • 1ºC = 1K 1824-1907 The Kelvin Temperature Scale (aka Absolute Scale) • The zero point on the Kelvin scale is absolute zero • 0K = -273ºC • Absolute zero is the point at which all molecular motion ceases. Lowest temperature possible. • Can absolute zero ever be reached? Converting between Celsius and Kelvin • ºC = K – 273 • At 50K air will freeze to a solid. Convert this to ºC. • ºC = 50 – 273 = -223 ºC • K = ºC + 273 • Antifreeze (ethylene glycol) boils at 199ºC. Convert this to K. • K = 199 + 273 = 472 K Comparing temperature scales • Note that in ºC, and K, there are 100 degrees between the freezing and boiling points of H20. • Note that in ºF there are 180º between the freezing and boiling points of H2O. • The Celsius scale begins 273.15º higher than Kelvin. • The Fahrenheit scale begins 32º higher than Celsius. Page 15 Derived units/ Ratios • Derived units are obtained by performing mathematical calculations on base units. • Example: Speed = distance time • What is the speed of a car (in mph) which travels 53miles in 48 minutes? – 53miles 60min = 66 miles/hour – 48min 1 hour Volume • The most commonly used metric unit used to express volume is the Liter (L). • The liter is not an SI unit. • The SI unit of volume is the cubic meter(m3). Too big to be convenient. Other units of volume. • • • • Cubic centimeter (cc or cm3) 1 cm3 = 1 mL Cubic decimeter (dm3) 1 dm3 = 1 L Density • Ratio of mass to volume • Calculated by dividing the mass of an object by its volume. • Density = mass volume · Expressed in g/cm3 · Based on water. 3 The density of pure H O is 1.00 g/cm · 2 Density • Example: If a metal block has a mass of 75g and a volume of 22 cubic centimeters, what is its density? 75g 22cm3 = 3.4 g/cm3 D. Density • An object has a volume of 825 cm3 and a density of 13.6 g/cm3. Find its mass. GIVEN: WORK: V = 825 cm3 D = 13.6 g/cm3 M=? M = DV M D V M = (13.6 g/cm3)(825cm3) M = 11,200 g D. Density • A liquid has a density of 0.87 g/mL. What volume is occupied by 25 g of the liquid? GIVEN: WORK: D = 0.87 g/mL V=? M = 25 g V=M D M D V V= 25 g 0.87 g/mL V = 29 mL 1.5 Uncertainty in Measurement • Exact numbers: known by counting or definition. Whole numbers and integers. • Inexact numbers: Derived from measurement. There is always estimation involved. The last digit is the uncertain digit. Scientific Method and Measurement Lesson 2: Scientific Measurement I. 1.5 Uncertainty in Measurement A. There is ambiguity in every measurement. Why? 1. Instruments are never completely free of flaws. (More expensive instruments are generally more accurate) 2. perfect Measuring involves estimation – because humans are reading, there may be human error!! Practice makes a. Digital Display – electronic balance b. Scale Display – grad. cylinder, thermometer, ruler * The last number in any measurement is estimated and therefore uncertain Accuracy is assessed by determining percent error % Error = [(Exp. Value – Accepted Value) / Accepted Value] x 100 * Note – the experimental value will be the average if more than one trial is performed for the experiment. Accuracy: how close a measurement is to the true or accepted value Precision: how reproducible the measurements are (how closely related the measurements are to each other) Accurate and Precise Precise, not accurate Accurate, not precise Neither accurate nor precise A. Accuracy vs. Precision • Accuracy - how close a measurement is to the accepted value • Precision - how close a series of measurements are to each other ACCURATE = CORRECT PRECISE = CONSISTENT Significant Figures • Used to indicate the exactness of a measurement. – 1cm vs. 1.0cm – 2.5s vs 2.52s • The final digit represents the estimated digit. • If using for a derived unit, the measure is only as accurate as the least accurate measurement. 1. Rules for Individual measurements a. All non-zero digits are significant. 1234 (4 siggy figs) b. All zeros between non-zero digits are significant. 101(3) c. Zeros to the right of a non-zero digit, but left of the decimal point are not significant unless specifically designated with a bar above it. 1100 vs 1100 d. Zeros to the right of the decimal point but to the left of a non-zero digit are not significant. .00038 e. Zeros to the right of the decimal point and following a non-zero digit are significant. 3.0027 * There will never be a bar on the right side of the decimal!! 2. Eg: How many significant figures for the measurements? a. 173.2 cm 4 _____ e. .025 L 2 _____ b. 205 kg 3 _____ f. 700 mL 1 _____ c. 4000 mm 1 _____ g. .090500 Mg 5 _____ d. 6.7 x 103 km 2 _____ 3. 4. Rules for Operations – Addition & Subtraction a. Perform operation, then round answer to the least accurate measurement (place value) for the measurements you are adding or subtracting. b. Eg: Perform the operation & then round the answer to the correct # of significant figures. 1.) 6.345 + 5.78 – 3.27 + 4.927 = 13.78 ________ 2.) .045 +.22 -.20 = ________ .07 Rules for Operations – Multiplication & Division a. b. Perform operation, then round answer to the least number of significant digits for the measurements given. Eg: Perform the operation and round answer to the correct # of significant figures. VII. 1.) 4.50 x .0062 .028 ________ 2.) (5.622)(72.3) / (320) 1.3 ________ 3.) (6.5 x 10-2) (3.27 x 10-3) 2.1 x 10-4 ________ 4.) (2.35)(.45723)(546) (379)(4.3 x 104) 3.6 x 10-5 ________ 1.6 Problem Solving A. Dimensional Analysis: technique for converting between units 1. Within the Metric System – move the decimal for how many jumps the multiple makes on the prefix chart 1-3 a. Ex: Convert 43 cm to . . . 1.) m .43 ________ 2.) km ________ 3.) um 430,000 ________ .00043 b. 2. Convert 276 g to . . . 1.) mg 276,000 ________ 2.) Mg .000276 ________ From metric to English or English to metric a. Write down what you are given b. Write down what you are working to c. Determine the conversion factor (unit equality) d. Cancel the units e. Do the arithmetic f. Convert the following; 1.) 47 miles to km 76 ________ 2.) 105 yards to m 96.0 ________ 3.) 75.2 kg to pounds 166 ________ 4.) 15 gallons to L 57 ________ Significant Digits B. Dimensional Analysis • The “Factor-Label” Method – Units, or “labels” are canceled, or “factored” out g cm g 3 cm 3 B. Dimensional Analysis • Steps: 1. Identify starting & ending units. 2. Line up conversion factors so units cancel. 3. Multiply all top numbers & divide by each bottom number. 4. Check units & answer. B. Dimensional Analysis • How many milliliters are in 1.00 quart of milk? qt mL 1.00 qt 1L 1000 mL 1.057 qt 1L = 946 mL B. Dimensional Analysis • You have 1.5 pounds of gold. Find its volume in cm3 if the density of gold is 19.3 g/cm3. cm3 lb 1.5 lb 1 kg 2.2 lb 1000 g 1 cm3 1 kg 19.3 g = 35 cm3 B. Dimensional Analysis • How many liters of water would fill a container that measures 75.0 in3? in3 75.0 L in3 (2.54 cm)3 1L (1 in)3 1000 cm3 = 1.23 L B. Dimensional Analysis 5) Your European hairdresser wants to cut your hair 8.0 cm shorter. How many inches will he be cutting off? cm in 8.0 cm 1 in 2.54 cm = 3.2 in B. Dimensional Analysis 6) Taft football needs 550 cm for a 1st down. How many yards is this? cm 550 cm yd 1 in 1 ft 2.54 cm 12 in 1 yd 3 ft = 6.0 yd B. Dimensional Analysis 7) A piece of wire is 1.3 m long. How many 1.5-cm pieces can be cut from this wire? cm 1.3 m pieces 100 cm 1 piece 1m 1.5 cm = 86 pieces