Download Chapter 28 Sources of the magnetic field

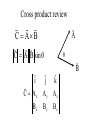
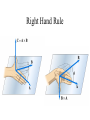
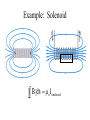
Chapter 30 Sources of the magnetic field
Force
Equation
Point
Object
Force
Point
Object
Field
Differential
Field
FG  mg
Gm1m 2
FG 
rˆ
2
r
kQ1Q 2
FE 
rˆ
2
r
Gm
g  2 rˆ
r
kQ
E  2 rˆ
r
Gdm
dg  2 rˆ
r
kdQ
dE  2 rˆ
r
FM  ?
B?
dB  ?
FE  qE
FM  qv  B
 I B
Is dB radial?
Does dB have 1/r2 dependence?
Biot-Savart Law – Set-Up
• The magnetic field is
dB at some point P
• The length element is
ds
• The wire is carrying a
steady current of I
o Ids  rˆ
dB 
4 r 2
Cross product review
C  AB
A
C  A B sin 
ˆi
C  Ax
Bx
ˆj
Ay
By

kˆ
Az
Bz
B
Right Hand Rule
Biot-Savart Law
o Ids  rˆ
dB 
2
4 r
o
7 T  m
km 
 1x10
4
A
Permeability of free space
For a long Wire:
ds
ˆi
ˆj
kˆ
ds  rˆ  0
dy 0  kˆ sin dy
sin  cos  0
Magnetic field of a long wire
o Ids  rˆ
dB 
4 r 2
 o I sin 
ˆ
dB  k
dy
2
4 r

R
tan  
y
o I sin 
ˆ
Bk
dy
2

4  r
o I
B
2 R
Magnetic field due to a straight wire
I
B
r
o I
B
2 r
Compare with:
2k
1 
E 

r
2 o r
B for a Curved Wire Segment
• Find the field at point O
due to the wire segment
• I and R are constants
μo I
B
θ
4πR
 will be in radians
Magnetic field due to a current loop
o Ids  rˆ
dB 
4 r 2
 o Ids
dB 
2
4 r
The perpendicular components
cancel by symmetry.
 o Ids
dB// 
cos 
2
4 r
o I
B// 
cos  ds 
2
4 r
 o IR 2
2R2  x
3
2 2

Magnetic field due to a current loop
At the center:
B(x  0) 
 o IR 2
2R2  x
o I

2R
3
2 2

x 0
Magnetic dipole moment vector
for a single loop:
  IA  IAnˆ
B
 o  IR 2  
2  R 2  x
When x>>R:
3
2 2


o
2  R 2  x
o
B
2x 3
3
2 2

Comparison to an electric dipole
-q
p 2a
+
E
 x 2  a 2 
q
B
Biot-Savart Law:
p
kp
E
 3
3
4o x
x
kp
3
2
o 
2  R 2  x
3
2 2

o 2k m
B
 3
3
2x
x
o Ids  rˆ
Id  rˆ
dB 
 km
2
2
4 r
r
5. Determine the magnetic field at a point P
located a distance x from the corner of an
infinitely long wire bent at a right angle, as
shown in Figure P30.5. The wire carries a
steady current I.
7. The segment of wire in Figure P30.7
carries a current of I = 5.00 A, where the
radius of the circular arc is R = 3.00 cm.
Determine the magnitude and direction of
the magnetic field at the origin.
10. A very long straight wire carries current
I. In the middle of the wire a right-angle
bend is made. The bend forms an arc of a
circle of radius r, as shown in Figure
P30.10. Determine the magnetic field at the
center of the arc.
Force between two parallel wires
FM  IL  B
a
 o I1
B1 
2 a
FM
FM
 I2 B1
o I1I2

2 a
Force between two parallel wires
FM
o I1I2

2 a
FM  I  B
If the currents are in the same
direction, the force is attractive.
If the currents are in the opposite
direction, the force is repulsive.
Historical definition of the Ampere
If 2 long parallel wires 1.0 m apart have the same
current in them and the force per unit length on each
wire is 2.0 x 10-7 N/m, the current is 1.0 Ampere
Historical definition of the Coulomb
If the current is 1.0 Ampere, then 1.0 Coulomb is the
amount of charge passing through a cross section in
1 second.
16. Two long, parallel conductors, separated by 10.0 cm, carry currents in the same
direction. The first wire carries current I1 = 5.00 A and the second carries I2 = 8.00
A. (a) What is the magnitude of the magnetic field created by I1 at the location of
I2? (b) What is the force per unit length exerted by I1 on I2? (c) What is the
magnitude of the magnetic field created by I2 at the location of I1? (d) What is the
force per length exerted by I2 on I1?
18. Two long, parallel wires are attracted to each other by a force per unit length of 320
μN/m when they are separated by a vertical distance of 0.500 m. The current in the
upper wire is 20.0 A to the right. Determine the location of the line in the plane of the
two wires along which the total magnetic field is zero.
63. Two long, parallel conductors carry currents in the same
direction as shown in Figure P30.63. Conductor A carries a
current of 150 A and is held firmly in position. Conductor B
carries a current IB and is allowed to slide freely up and
down (parallel to A) between a set of nonconducting guides.
If the mass per unit length of conductor B is 0.100 g/cm,
what value of current IB will result in equilibrium when the
distance between the two conductors is 2.50 cm?
Introduction to Ampere’s Law
b
Recall the definition of electric potential:
Vba    E ds
a
What is the value of the integral over a closed path for any
electric field?
a
Vaa    E ds    E ds  ?
a
Let’s try the same thing for a magnetic field
around a current carrying wire.
 B ds  
o I
o I
ds 
2r   o I
2 r
2 r
Ampere’s Law
 B ds   I
o enclosed
This result has been shown
experimentally to be true in general
• The integral is around any closed path
• The current is that passing through the surface bounded by
the path
• Like Gauss’s Law, useful in finding fields for highly
symmetric problems
Applying Ampere’s Law
Qenclosed
 E   E dA 
o
• Select a surface
– Try to imagine a surface where
the electric field is constant
everywhere. This is
accomplished if the surface is
equidistant from the charge.
– Try to find a surface such that
the electric field and the
normal to the surface are either
perpendicular or parallel.
• Determine the charge inside
the surface
• If necessary, break the
integral up into pieces and
sum the results.
 B ds   I
o enclosed
• Select a path
– Try to imagine a path where the
magnetic field is constant
everywhere. This is accomplished
if the surface is equidistant from
the charge.
– Try to find a path such that the
magnetic field and the path are
either perpendicular or parallel.
• Determine the current inside
the surface
• If necessary, break the
integral up into pieces and
sum the results.
Example: Magnetic field inside a wire
B
ds


I
o
enclosed

Iencl r

I
R 2
2
r
B 2r  o I 2
R
2
 o Ir
B
2
2R
Example: Solenoid
 B ds   I
o enclosed
Example: Solenoid
Bd
b
c
  o Ienclosed
0d
0
a
 Bsmallds   B ds   B ds   B ds   NI
o
a
b
B
 o NI
c
d
B  o
N
I   o nI
Example: Toroid
Bd
  o Ienclosed
Inside:
B  2r   o NI
 o NI
B
2r
Outside:
B 0
21. Four long, parallel conductors carry equal currents of I =
5.00 A. Figure P30.21 is an end view of the conductors. The
current direction is into the page at points A and B (indicated
by the crosses) and out of the page at C and D (indicated by
the dots). Calculate the magnitude and direction of the
magnetic field at point P, located at the center of the square
of edge length 0.200 m.
29. A long cylindrical conductor of radius R carries a
current I as shown in Figure P30.29. The current density
J, however, is not uniform over the cross section of the
conductor but is a function of the radius according to J =
br, where b is a constant. Find an expression for the
magnetic field B (a) at a distance r1 < R and (b) at a
distance r2 > R, measured from the axis.
24. The magnetic field 40.0 cm away from a long straight wire carrying current 2.00
A is 1.00 μT. (a) At what distance is it 0.100 μT? (b) What If? At one instant, the two
conductors in a long household extension cord carry equal 2.00-A currents in
opposite directions. The two wires are 3.00 mm apart. Find the magnetic field 40.0
cm away from the middle of the straight cord, in the plane of the two wires. (c) At
what distance is it one tenth as large? (d) The center wire in a coaxial cable carries
current 2.00 A in one direction and the sheath around it carries current 2.00 A in the
opposite direction. What magnetic field does the cable create at points outside?
Magnetic Flux
•
•
•
•
The magnetic field in this element is B
dA is a vector that is perpendicular to the surface
dA has a magnitude equal to the area dA
The magnetic flux B is
 B   B  dA
• The unit of magnetic flux is T.m2 = Wb
– Wb is a weber
Gauss’ Law in Magnetism
• Magnetic fields do not begin or end at any
point
– The number of lines entering a surface equals
the number of lines leaving the surface
• Gauss’ law in magnetism says:
 B   B  dA  0
Displacement Current
• Ampere’s law in the original form
is valid only if any electric fields
present are constant in time
• Maxwell added an additional term
which includes a factor called the
displacement current, Id
• The displacement current is not the
current in the conductor
– Conduction current will be used to
refer to current carried by a wire or
other conductor
Bd
  o Ienclosed
dE
I d  εo
dt
Ampere’s Law – General Form
• Also known as the Ampere-Maxwell law
dE
 B  ds  μo  I  I d   μo I  μoεo dt
• Magnetic fields are produced both by
conduction currents and by time-varying
electric fields
Ferromagnetism
• Domains
• Curie Temperature
• Electron orbits align
with an external
magnetic field