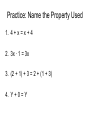Download real number properties

Warm Up
Place the following numbers
in ascending order, then circle
the integers.
½, -2, -12/3, ¾, 0.3, 0, 5/5
Hint: Use your calculator to turn the fractions into decimals; this will help you put
them in the right order.
The Real Number System
Essential Question:
How do we use the real number properties to
rewrite algebraic expressions?
The Real Number System
• The rational and irrational numbers
together make the real number system
• There are six real number properties that
are true for all of the real numbers
The Real Number Properties
•
•
•
•
•
•
Identity
Commutative
Associative
Distributive
Additive Inverse
Multiplicative Inverse (reciprocal)
Identity
• There are two kinds of identities
– Additive: 0
– Multiplicative: 1
• The identity, keeps a number the same
• 3 + 0 = 3 (additive identity)
• 4 x 1 = 4 (multiplicative identity)
Commutative Property
• The word “commute” means to travel back
and forth
• Works for addition and multiplication
• Addition: A + B = B + A
• Multiplication: AB = BA
Practice: Rewrite the following
expressions using the commutative
property
• X+3=
3+x
• 3∙5=
5∙3
• -3 + 2x = 2x + (-3) = 2x - 3
Associative Property
• The word “associate” means to group
• Works for addition and multiplication
• Addition: (A + B) + C = A + (B + C)
• Multiplication: A(BC) = (AB)C
Practice: Rewrite the following
expressions using the associative
property
• X + (3 + 2y) =
(x + 3) + 2y
• 3 ∙ (5 ∙ 12) =
(3 ∙ 5) ∙ 12
• 4 + (2x + 2y) =
(4 + 2x) + 2y
Practice: Name the Property Used
1. 4 + x = x + 4
2. 3x ∙ 1 = 3x
3. (2 + 1) + 3 = 2 + (1 + 3)
4. Y + 0 = Y
Distributive Property
• Works across addition and subtraction
• Addition: A (B + C) = AB + AC
• Subtraction: A(B – C) = AB - AC
Practice: Rewrite the following
expressions using the distributive
property
• 3(x + 5) =
3x + 15
• 2 ∙ (x - 12) =
2x - 24