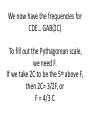Download Document

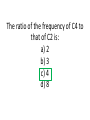
L8
Musical Scales, Chords , and
Intervals,
The Pythagorean and Just Scales
Musical Intervals (roughly in order of decreasing consonance)
Name of
Interval
Notes
(in key of C
major)
Pythagorean
Frequency
Ratios
Just
Frequency
Ratios
# Semitones
(on equaltempered
scale)
Octave
C↔C
2
2
12
Fifth
C↔G
3/2
6/4 = 3/2
7
Fourth
C↔F
4/3
Major Third
C↔E
81/64
Minor Third
E↔G
Major Sixth
C↔A
Minor Sixth
E↔C
Tonic
C
5
5/4
4
3
27/16
9
8
1
4/4 = 1
none
* a semitone interval corresponds to a frequency difference of about 6%
C
D
E
F
G
A
B
C
* The white notes of the piano give the seven notes of the C-major diatonic scale.
The ratio of the frequency of C4 to
that of C2 is:
a) 2
b) 3
c) 4
d) 8
The ratio of the frequency of C4 to
that of C2 is:
a) 2
b) 3
c) 4
d) 8
One octave of the diatonic scale
including the tonic and the octave
note contains:
a) 5 notes
b) 6 notes
c) 7 notes
d) 8 notes
One octave of the diatonic scale
including the tonic and the octave
note contains:
a) 5 notes
b) 6 notes
c) 7 notes
d) 8 notes
One octave of the chromatic scale
(including the octave note)
contains:
a) 8 notes
b) 10 notes
c) 11 notes
d) 12 notes
e) 13notes
One octave of the chromatic scale
(including the octave note)
contains:
a) 8 notes
b) 10 notes
c) 11 notes
d) 12 notes
e) 13notes
A musical scale is a systematic arrangement of pitches
Each musical note has a perceived pitch with a particular frequency
(the frequency of the fundamental)
Going up or down in frequency, the perceived pitch follows a pattern
One cycle of pitch repetition is called an octave.
The interval between successive pitches determines the type of scale.
Intervals
12-tone scale (chromatic)
8-tone scale (diatonic)
Note span
C-C
C - C#
C-D
C - D#
C-E
C-F
C - F#
C-G
C - G#
C-A
C - A#
C-B
C3 - C 4
C3 - E4
Interval
Frequency ratio
unison
1/1
semitone
16/15
whole tone (major second)
9/8
minor third
6/5
major third
5/4
perfect fourth
4/3
augmented fourth
45/32
perfect fifth
3/2
minor sixth
8/5
major sixth
5/3
minor seventh
16/9 (or 7/4)
major seventh
15/8
octave
2/1
octave+major third
5/2
compound
intervals
Adding intervals means multiplying frequency ratios
major third + minor third
perfect fourth + perfect fifth
perfect fourth + major third
perfect fourth + whole tone
5 6 30 3
=
× =
4 5 20 2
4 3 12 2
× = =
3 2 6 1
4 5 20 5
× =
=
3 4 12 3
5 16 80 4
× =
=
4 15 60 3
perfect fifth
octave
major sixth
perfect fourth
more compound intervals
ratios larger than 2 can be split up into an octave + something
perfect fifth + perfect fifth
major seventh + minor sixth
3 3 9 2 9
× = = ×
2 2 4 1 8
15 8 15 3 2 3
× = = = ×
8 5 5 1 1 2
Octave + whole tone
Octave + perfect fifth
Consonant intervals
Overlapping harmonics
tonic
120
240
octave
fifth
fourth
360
480
240
480
180
160
600
360
M third
150
300
m third
144
288
840
720
900
640
800
450600
750
900
576 720
1080
960
480
432
960
720
540
320
720
864
1080
960
1050
1008
Dissonant intervals
Perceived when harmonics are close enough for beating
harmonic series
Intervals between consecutive harmonics
Fundamental
2nd
f1
harmonic
f2 = 2f1
octave
3rd harmonic
f3 = 3f1
perfect fifth
4th harmonic
f4 = 4f1
perfect fourth
5th harmonic
f5 = 5f1
major third
6th harmonic
f6 = 6f1
minor third
f2 2
=
f1 1
f3 3
=
f2 2
f4 4
=
f3 3
f5 5
=
f4 4
f6 6
=
f5 5
CT 2.4.5
What is the name of the note that is a major 3rd
above E4=330 Hz?
A: G
B: G#
C: A
D: A#
E: B
CT 2.4.5
What is the name of the note that is a major 3rd
above E4=330 Hz?
A: G
B: G#
C: A
D: A#
E: B
Intervals
C- D, a second
C-E, a third
C-F, a 4th
C-G, a 5th,
C-A, a 6th
C-B, a (major) 7th,
C-2C, an octave
C-2D, a 9th
C-2E, a 10th,
C-2F, an 11th,
C-2G, a 12th,
C-2A, a 13th, etc.
C-Eb, a minor 3rd
C-Bb, a dominant 7th,
C-2Db, a flatted 9th, etc.
Pythagorean Scale
Built on 5ths
A pleasant consonance was observed
playing strings whose lengths were
related by the ratio of 3/2 to 1 (demo).
Let’s call the longer string C, and the
shorter G,
and the interval between G and C a 5th
Denote the frequency of C simply by
the name C, etc.
Since f1= V/2L, and LC= 3/2 LG,
G =3/2C.
Similarly a 5th above G is 2D, and
D= 1/2 (3/2G)= 9/8 C.
Then A is 3/2 D= 27/16 C.
Then 2E= 3/2 A or E= 81/64 C, and
B=3/2 E = 243/128 C.
We now have the frequencies for
CDE… GAB(2C)
To fill out the Pythagorean scale,
we need F.
If we take 2C to be the 5th above F,
then 2C= 3/2F, or
F = 4/3 C
Just Scale, Built on Major
Triads
We take 3 sonometers to play 3 notes
to make a major triad, e.g. CEG. This
sounds consonant (and has been the
foundation of western music for
several hundred years), and we
measure the string lengths required
for this triad.
We find (demo) that the string
lengths have ratios 6:5:4 for the
sequence CEG.
The major triad is the basis for the
just scale, which we now develop
in a way similar to that of the
Pythagorean scale.
CT 2.4.5
Suppose we start a scale at
E4=330 Hz. What frequency is a (just) perfect 5th
above this?
A 1650 Hz
B: 220 Hz
C: 495 Hz
D: 660 Hz
E: None of these
CT 2.4.5
Suppose we start a scale at
E4=330 Hz. What frequency is a (just) perfect 5th
above this?
A 1650 Hz
B: 220 Hz
C: 495 Hz
D: 660 Hz
E: None of these
CT 2.4.5
What is the frequency of the note that is a (just)
major 3rd above E4=330 Hz?
A: 660 Hz
B: 633 Hz
C: 512 Hz
D: 440 Hz
E: 412 Hz
CT 2.4.5
What is the frequency of the note that is a (just)
major 3rd above E4=330 Hz?
A: 660 Hz
B: 633 Hz
C: 512 Hz
D: 440 Hz
E: 412 Hz
CT 2.4.5
Suppose we start a scale at
E4=330 Hz. What frequency is a (just) perfect 5th
below this?
A 165 Hz
B: 220 Hz
C: 110 Hz
D: 66 Hz
E: None of these
CT 2.4.5
Suppose we start a scale at
E4=330 Hz. What frequency is a (just) perfect 5th
below this?
A 165 Hz
B: 220 Hz
C: 110 Hz
D: 66 Hz
E: None of these