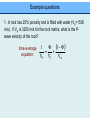Download CHAPTER 2 – Seismic waves

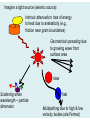
CHAPTER 2 – Seismic waves
2.1 Introduction to waves
A wave:
• is a periodic disturbance
• transmits energy through a material
• no permanent deformation
!
Seismic waves:
• transmit elastic strain energy
(stretching, tearing, bending, distortion across
some surface…)
• generated by a seismic source (explosion, vibroseis,
earthquake…)
View 1: Snapshot of displacement
v = velocity (m/s)
à speed at which
the wave travels
A = amplitude (m)
à maximum
displacement from
rest position
λ = wavelength (m)
à distance
between two points
with same phase
(e.g., peaks, troughs)
View 2: Plot particle displacement through time
T = period (s)
à time for one
complete cycle
(oscillation)
f = frequency (s-1, Hz)
à number of cycles
per second (=1/T)
Angular frequency:
ω = 2πf (rad s-1)
View 1
View 2
20 m
20m
The two views are complementary:
v=d/t and v=fλ
Remark: Seismic waves are sensitive to structure
of similar wavelengths or greater.
Question: Given a simple structure (v) and survey wave
frequency, do you know the rough resolution of a survey?
Seismic wave propagation
In seismic exploration,
we determine how
seismic waves have
travelled from the
seismic source to the
detector.
à changes in velocity,
propagation direction,
and wave amplitude
indicate changes in
subsurface geology.
• wavefront = locus of points with
the same phase (expands
spherically)
• ray = vector showing direction of
travel of one point (perpendicular to
wavefront)
Huygens principle:
• each point on wavefront
acts as a point source
• spherical waves radiate
outward from each point
source
• envelope of waves is the
overall wavefront
Fermat’s Principle:
• rays propagate along the
path which yields the
smallest travel time
(principle of least time)
Constant
velocity
Hitchhike on a highway during a summer day
Question: Why is your view so fuzzy on a hot
summer day?
Types of seismic waves
Body waves: travel through the interior of the Earth
P-waves – compressional waves (longitudinal, primary)
• particle motion is in the direction of propagation (e.g., sound waves)
• fastest seismic waves (VP)
(http://web.ics.purdue.edu/~braile/edumod/waves/WaveDemo.htm;
see also Fig 2.7 in textbook)
S-waves – shear waves (transverse, secondary)
• particle motion is perpendicular to the direction of propagation
• two polarizations: SH-waves and SV-waves
• velocity (VS) is less than VP
(http://web.ics.purdue.edu/~braile/edumod/waves/WaveDemo.htm;
see also Fig 2.8 in textbook)
Surface waves: travel along interfaces, such as the ground
Rayleigh waves (“ground roll”)
• coupling between P and S waves at an interface
• elliptical retrograde particle motion in vertical plane
• amplitude decreases exponentially
• velocity (VR) is lower than VS
(http://web.ics.purdue.edu/~braile/edumod/waves/WaveDemo.htm;
see also Fig 2.10a in textbook)
Rayleigh waves are dispersive (VR depends on frequency)
à lower frequency Rayleigh waves have a higher velocity because they
extend to greater depths
Seismic recordings of the collapse of
the World Trade Centre
(Kim et al., EOS, 2001;
www.ldeo.columbia.edu/
~mwest/papers/
WTC_LDEO_KIM.pdf)
Dispersion and frequency-dependent depth sensitivity
.
Love waves
• generated when a near-surface layer has a lower VS than underlying layer
• trapped shear waves with velocity intermediate between VS of two layers
• horizontal particle motion perpendicular to direction of travel
• dispersive
(http://web.ics.purdue.edu/~braile/edumod/waves/WaveDemo.htm;
see also Fig 2.10b in textbook)
Seismic velocities of rocks
• seismic source releases energy as a wave
• as it passes through a material, it exerts stress
• causes small deformation (strain)
• strain is elastic – not permanent
!
Stress = force per unit area (pressure) – N/m2 or Pa
Strain = fractional change in shape – dimensionless
!
Hooke’s Law: strain is proportional to the stress that
produced it (linear elasticity)
For a spring: F = k Δx
where k is the spring constant (material property)
à k governs how much stress is needed to
produce a given strain
For seismic waves: stress-strain relationship given by the elastic parameters
(moduli) of the rocks – measure of strength/rigidity of the rocks
• force needed to shorten by • volume change
ΔL:
under 3D pressure:
ψ=
long. stress (F/A)
long. strain (ΔL/L)
Can show:
K=
volume stress (P)
vol. change (ΔV/V)
4
ψ=K+ µ
3
• shear strain due
to shearing:
µ=
shear stress (τ)
shear strain
(tan θ)
stronger material is harder to
deform à larger ψ, K, and µ
P-wave:
F
a longitudinal wave
(another: sound wave)
Longitudinal modulus (ψ):
4
ψ=K+ µ
3
&ψ#
VP = $$ !!
%ρ"
1
2
4 #
&
$K+ µ!
3 !
=$
$ ρ !
$
!
%
"
1
2
S-wave:
F
Shear
modulus (µ):
(rotated 90°)
&µ#
VS = $$ !!
%ρ"
1
2
P-waves
"
4 %
$K + µ'
3 '
VP = $
$ ρ '
#
&
S-waves
1
2
"µ %
VS = $ '
#ρ&
1
2
• VP is always larger than VS
• stronger material à
larger ψ, K, and µ à
larger VP and VS
• VP and VS decrease as density increases
• VP and VS do not depend on frequency (non-dispersive)
• in fluids, µ=0 (and K>0) à
only P-waves travel through fluids (VS =0)
Question: Why does velocity increase with depth?
Poisson’s Ratio (σ)
• σ = lateral strain / longitudinal strain
• can show:
!
!
VP & 2(1 − σ )#
=$
VS % (1 − 2σ )!"
1
2
• in consolidated crustal rocks, σ ~0.25 à
VP/VS ~1.7
• Poisson’s ratio is strongly affected by the presence of fluids,
possibly age.
Global Observations
mafic rocks: > 0.25
felsic rocks: < 0.25
Zandt and Ammon, 1995, Nature
Mafic is used for silicate minerals, magmas, and rocks which are relatively high in the heavier elements,
magnesium, iron, sodium, calcium.
Felsic rocks is used for silicate minerals, magmas, and rocks which have a lower percentage of the
)21
heavier elements, and are correspondingly enriched in the lighter elements, such as silicon and oxygen,
aluminum, and potassium
Factors that control VP of rocks (m/s)
Air
340
Water
1400-1600
Petroleum
1300-1400
Sand (unsaturated) 200-1000
Sandstones
Tertiary
2000-2500
• density and elastic moduli
depend primarily on composition
!
• VP increases as rocks become
more mafic (granite-gabbroultramafic)
Carboniferous 4000-4500
Limestones
Cretaceous 2000-2500
Jurassic
3000-4000
Carboniferous 5000-5500
Salt
4500-5000
Granite
5000-6000
Basalt
5400-6400
Ultramafic rocks
7500-8500
&ψ#
VP = $$ !!
%ρ"
1
2
4 #
&
$K+ µ!
3 !
=$
$ ρ !
$
!
%
"
1
2
from www.talkorigins.org
)23
Factors that control VP of rocks (m/s)
Air
340
Water
1400-1600
Petroleum
1300-1400
Sand (unsaturated) 200-1000
Sandstones
Tertiary
2000-2500
Carboniferous 4000-4500
Limestones
Cretaceous 2000-2500
Jurassic
3000-4000
Carboniferous 5000-5500
Salt
4500-5000
Granite
5000-6000
Basalt
5400-6400
Ultramafic rocks
7500-8500
• sedimentary rocks tend to
have lower VP
à depends mostly on the
porosity of the rocks
VP increases with age à
increase in rigidity with
cementation
Effect of porosity on velocity
• rock is composed of rock matrix and pore
space (often filled with fluid/air that has low
velocity)
• porosity (Φ) is the fractional volume occupied
by pore space
• velocity decreases with increasing Φ
(Sherriff and
Geldart, 1995)
Effect of porosity on velocity
• the overall rock properties are the average of the matrix (m) and pore
fluid (f) properties, weighted by Φ
• EXAMPLE: for density: ρ = ρf Φ + (1- Φ) ρm
!
• for velocity: weight by the amount of time that seismic wave spends in the
rock matrix and pore fluid (v = d/t à t = d/v)
time-average
equation:
1
Φ (1 − Φ )
=
+
VP Vf
Vm
)26
Effect of depth on seismic velocity
• seismic velocities generally increase with
depth:
• increased compaction – reduces pore
space
• elastic moduli increase with pressure
Reconstructing basin history:
(http://gsc.nrcan.gc.ca/gashydrates/
westvanisland/index_e.php)
(Sheriff and Geldart, 1995)
Example questions
1. A rock has 25% porosity and is filled with water (VP=1500
m/s). If VP is 3200 m/s for the rock matrix, what is the Pwave velocity of the rock?
time-average
equation:
1
Φ (1 − Φ )
=
+
VP Vf
Vm
Example questions
2. Gas-filled sandstone:
Sandstone matrix
Gas pore fluid
4300 m/s
300 m/s
If the overall VP is 2200 m/s, what is the porosity?
time-average
equation:
1
Φ (1 − Φ )
=
+
VP Vf
Vm
Factors that affect seismic wave amplitude
Seismic exploration:
Travel time &
amplitude of
seismic waves
Subsurface
velocity
structure
Subsurface
geology
Three factors that cause seismic wave amplitudes to decrease
between source and receiver:
1. Geometrical spreading
2. Multipathing
3. Scattering
4. Intrinsic attenuation
(AND…as waves pass into different materials, partitioning of
energy at the interface affects amplitude....Sections 4.1 and 4.2)
Imagine a light source (seismic source):
Intrinsic attenuation: loss of energy
to heat due to anelasticity (e.g.,
friction near grain boundaries)
Geometrical spreading due
to growing wave front
surface area
slow
Scattering when
wavelength ~ particle
dimension
fast
Multipathing due to high & low
velocity bodies (ala Fermat)
1. Geometrical spreading (spherical divergence)
Seismic energy (E0) spreads
out from a point source
(e.g., explosion) as a
spherical wavefront
• the wavefront always contains a constant amount of energy (E0)
• the energy at a point on the sphere surface is: E(r) = E0 / 4πr2
(where r is the distance from the source)
• amplitude of a seismic wave is related to energy: E(r) α A2
• since E(r) α 1/r2 à
A2 α 1/r2 à
A α 1/r
à in order to conserve energy, seismic wave amplitude must
decrease by 1/r
Body wave propagation
One person’s noise is
another person’s signal.
This is certainly true for
what surface waves
mean to an exploration
geophysicist and to a
global seismologist
Surface Wave Propagation
Amplitude decay in surface
waves (as a function of r) is
less than that of body wave --(by square root of r), the
main reason that we always
find larger surface waves than
body waves, especially at
long distances.
33
2. Attenuation (absorption)
• seismic wave propagation is not completely elastic
• small fraction of seismic energy is converted to frictional heat
• loss of energy = decrease in amplitude
• characterize this with the “quality factor” (Q):
!
!
!
2πE
Q=
ΔE
• Q is a measure of the fractional loss of energy per cycle (oscillation)
of the seismic wave
• high Q mean little energy loss
• can show that the loss of energy will cause an exponential decrease
in seismic wave amplitude over time (t):
!
!
A( t ) = A 0 e
− πft
Q
(e is the exponential constant 2.718)
• note that this is a function of frequency
• higher frequency = more cycles per second = more energy lost
• can also write in terms of distance traveled by wave (x):
!
!
!
à
A( x ) = A 0 e
− πx
Qλ
amplitude decays more rapidly for: low Q or high f (short λ)
(Material)
(Seismic wave)
Example of attenuation:
Common approach to calculate Q
Interpretation 1:
Suppose A0 represents wave amplitude, then
A = A0e−bt = A0e−ω 0 t /(2Q )
ln(A)
$ω 0 '
ln(A) = ln(A0 ) − & )t
%2Q(
€
intercept
slope
t
€
Star Track
!
The Q
)37
The Earth is more
attenuating than the
Moon.
!
Problem: where are
P, S, Surf. waves?
)38
• seismic sources release energy
over a wide range of frequencies
(Kearey et al., 2002)
• as wave travels, the high frequency
components will be more strongly
attenuated
• over time, wave is dominated by
low frequency (long wavelength)
components à seismic wave will
become smoother and more spread
out over time
(similar to thunder)
• for crustal rocks, Q is typically 100-200
• QP > QS à energy loss caused mostly by shear deformation
3. Scattering
• most materials contain small heterogeneities
• grains, mineral boundaries, pore edges, cracks, etc.
• some seismic energy is scattered when it encounters these features
• therefore amplitude will decrease
Wavelength effect demonstrated for P wave coda. People use source spectrum
to analyze the coda and obtain information about Q and scatters about a given
path