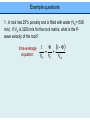* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download CHAPTER 2 – Seismic waves
Survey
Document related concepts
Transcript
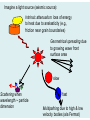
CHAPTER 2 – Seismic waves 2.1 Introduction to waves A wave: • is a periodic disturbance • transmits energy through a material • no permanent deformation ! Seismic waves: • transmit elastic strain energy (stretching, tearing, bending, distortion across some surface…) • generated by a seismic source (explosion, vibroseis, earthquake…) View 1: Snapshot of displacement v = velocity (m/s) à speed at which the wave travels A = amplitude (m) à maximum displacement from rest position λ = wavelength (m) à distance between two points with same phase (e.g., peaks, troughs) View 2: Plot particle displacement through time T = period (s) à time for one complete cycle (oscillation) f = frequency (s-1, Hz) à number of cycles per second (=1/T) Angular frequency: ω = 2πf (rad s-1) View 1 View 2 20 m 20m The two views are complementary: v=d/t and v=fλ Remark: Seismic waves are sensitive to structure of similar wavelengths or greater. Question: Given a simple structure (v) and survey wave frequency, do you know the rough resolution of a survey? Seismic wave propagation In seismic exploration, we determine how seismic waves have travelled from the seismic source to the detector. à changes in velocity, propagation direction, and wave amplitude indicate changes in subsurface geology. • wavefront = locus of points with the same phase (expands spherically) • ray = vector showing direction of travel of one point (perpendicular to wavefront) Huygens principle: • each point on wavefront acts as a point source • spherical waves radiate outward from each point source • envelope of waves is the overall wavefront Fermat’s Principle: • rays propagate along the path which yields the smallest travel time (principle of least time) Constant velocity Hitchhike on a highway during a summer day Question: Why is your view so fuzzy on a hot summer day? Types of seismic waves Body waves: travel through the interior of the Earth P-waves – compressional waves (longitudinal, primary) • particle motion is in the direction of propagation (e.g., sound waves) • fastest seismic waves (VP) (http://web.ics.purdue.edu/~braile/edumod/waves/WaveDemo.htm; see also Fig 2.7 in textbook) S-waves – shear waves (transverse, secondary) • particle motion is perpendicular to the direction of propagation • two polarizations: SH-waves and SV-waves • velocity (VS) is less than VP (http://web.ics.purdue.edu/~braile/edumod/waves/WaveDemo.htm; see also Fig 2.8 in textbook) Surface waves: travel along interfaces, such as the ground Rayleigh waves (“ground roll”) • coupling between P and S waves at an interface • elliptical retrograde particle motion in vertical plane • amplitude decreases exponentially • velocity (VR) is lower than VS (http://web.ics.purdue.edu/~braile/edumod/waves/WaveDemo.htm; see also Fig 2.10a in textbook) Rayleigh waves are dispersive (VR depends on frequency) à lower frequency Rayleigh waves have a higher velocity because they extend to greater depths Seismic recordings of the collapse of the World Trade Centre (Kim et al., EOS, 2001; www.ldeo.columbia.edu/ ~mwest/papers/ WTC_LDEO_KIM.pdf) Dispersion and frequency-dependent depth sensitivity . Love waves • generated when a near-surface layer has a lower VS than underlying layer • trapped shear waves with velocity intermediate between VS of two layers • horizontal particle motion perpendicular to direction of travel • dispersive (http://web.ics.purdue.edu/~braile/edumod/waves/WaveDemo.htm; see also Fig 2.10b in textbook) Seismic velocities of rocks • seismic source releases energy as a wave • as it passes through a material, it exerts stress • causes small deformation (strain) • strain is elastic – not permanent ! Stress = force per unit area (pressure) – N/m2 or Pa Strain = fractional change in shape – dimensionless ! Hooke’s Law: strain is proportional to the stress that produced it (linear elasticity) For a spring: F = k Δx where k is the spring constant (material property) à k governs how much stress is needed to produce a given strain For seismic waves: stress-strain relationship given by the elastic parameters (moduli) of the rocks – measure of strength/rigidity of the rocks • force needed to shorten by • volume change ΔL: under 3D pressure: ψ= long. stress (F/A) long. strain (ΔL/L) Can show: K= volume stress (P) vol. change (ΔV/V) 4 ψ=K+ µ 3 • shear strain due to shearing: µ= shear stress (τ) shear strain (tan θ) stronger material is harder to deform à larger ψ, K, and µ P-wave: F a longitudinal wave (another: sound wave) Longitudinal modulus (ψ): 4 ψ=K+ µ 3 &ψ# VP = $$ !! %ρ" 1 2 4 # & $K+ µ! 3 ! =$ $ ρ ! $ ! % " 1 2 S-wave: F Shear modulus (µ): (rotated 90°) &µ# VS = $$ !! %ρ" 1 2 P-waves " 4 % $K + µ' 3 ' VP = $ $ ρ ' # & S-waves 1 2 "µ % VS = $ ' #ρ& 1 2 • VP is always larger than VS • stronger material à larger ψ, K, and µ à larger VP and VS • VP and VS decrease as density increases • VP and VS do not depend on frequency (non-dispersive) • in fluids, µ=0 (and K>0) à only P-waves travel through fluids (VS =0) Question: Why does velocity increase with depth? Poisson’s Ratio (σ) • σ = lateral strain / longitudinal strain • can show: ! ! VP & 2(1 − σ )# =$ VS % (1 − 2σ )!" 1 2 • in consolidated crustal rocks, σ ~0.25 à VP/VS ~1.7 • Poisson’s ratio is strongly affected by the presence of fluids, possibly age. Global Observations mafic rocks: > 0.25 felsic rocks: < 0.25 Zandt and Ammon, 1995, Nature Mafic is used for silicate minerals, magmas, and rocks which are relatively high in the heavier elements, magnesium, iron, sodium, calcium. Felsic rocks is used for silicate minerals, magmas, and rocks which have a lower percentage of the )21 heavier elements, and are correspondingly enriched in the lighter elements, such as silicon and oxygen, aluminum, and potassium Factors that control VP of rocks (m/s) Air 340 Water 1400-1600 Petroleum 1300-1400 Sand (unsaturated) 200-1000 Sandstones Tertiary 2000-2500 • density and elastic moduli depend primarily on composition ! • VP increases as rocks become more mafic (granite-gabbroultramafic) Carboniferous 4000-4500 Limestones Cretaceous 2000-2500 Jurassic 3000-4000 Carboniferous 5000-5500 Salt 4500-5000 Granite 5000-6000 Basalt 5400-6400 Ultramafic rocks 7500-8500 &ψ# VP = $$ !! %ρ" 1 2 4 # & $K+ µ! 3 ! =$ $ ρ ! $ ! % " 1 2 from www.talkorigins.org )23 Factors that control VP of rocks (m/s) Air 340 Water 1400-1600 Petroleum 1300-1400 Sand (unsaturated) 200-1000 Sandstones Tertiary 2000-2500 Carboniferous 4000-4500 Limestones Cretaceous 2000-2500 Jurassic 3000-4000 Carboniferous 5000-5500 Salt 4500-5000 Granite 5000-6000 Basalt 5400-6400 Ultramafic rocks 7500-8500 • sedimentary rocks tend to have lower VP à depends mostly on the porosity of the rocks VP increases with age à increase in rigidity with cementation Effect of porosity on velocity • rock is composed of rock matrix and pore space (often filled with fluid/air that has low velocity) • porosity (Φ) is the fractional volume occupied by pore space • velocity decreases with increasing Φ (Sherriff and Geldart, 1995) Effect of porosity on velocity • the overall rock properties are the average of the matrix (m) and pore fluid (f) properties, weighted by Φ • EXAMPLE: for density: ρ = ρf Φ + (1- Φ) ρm ! • for velocity: weight by the amount of time that seismic wave spends in the rock matrix and pore fluid (v = d/t à t = d/v) time-average equation: 1 Φ (1 − Φ ) = + VP Vf Vm )26 Effect of depth on seismic velocity • seismic velocities generally increase with depth: • increased compaction – reduces pore space • elastic moduli increase with pressure Reconstructing basin history: (http://gsc.nrcan.gc.ca/gashydrates/ westvanisland/index_e.php) (Sheriff and Geldart, 1995) Example questions 1. A rock has 25% porosity and is filled with water (VP=1500 m/s). If VP is 3200 m/s for the rock matrix, what is the Pwave velocity of the rock? time-average equation: 1 Φ (1 − Φ ) = + VP Vf Vm Example questions 2. Gas-filled sandstone: Sandstone matrix Gas pore fluid 4300 m/s 300 m/s If the overall VP is 2200 m/s, what is the porosity? time-average equation: 1 Φ (1 − Φ ) = + VP Vf Vm Factors that affect seismic wave amplitude Seismic exploration: Travel time & amplitude of seismic waves Subsurface velocity structure Subsurface geology Three factors that cause seismic wave amplitudes to decrease between source and receiver: 1. Geometrical spreading 2. Multipathing 3. Scattering 4. Intrinsic attenuation (AND…as waves pass into different materials, partitioning of energy at the interface affects amplitude....Sections 4.1 and 4.2) Imagine a light source (seismic source): Intrinsic attenuation: loss of energy to heat due to anelasticity (e.g., friction near grain boundaries) Geometrical spreading due to growing wave front surface area slow Scattering when wavelength ~ particle dimension fast Multipathing due to high & low velocity bodies (ala Fermat) 1. Geometrical spreading (spherical divergence) Seismic energy (E0) spreads out from a point source (e.g., explosion) as a spherical wavefront • the wavefront always contains a constant amount of energy (E0) • the energy at a point on the sphere surface is: E(r) = E0 / 4πr2 (where r is the distance from the source) • amplitude of a seismic wave is related to energy: E(r) α A2 • since E(r) α 1/r2 à A2 α 1/r2 à A α 1/r à in order to conserve energy, seismic wave amplitude must decrease by 1/r Body wave propagation One person’s noise is another person’s signal. This is certainly true for what surface waves mean to an exploration geophysicist and to a global seismologist Surface Wave Propagation Amplitude decay in surface waves (as a function of r) is less than that of body wave --(by square root of r), the main reason that we always find larger surface waves than body waves, especially at long distances. 33 2. Attenuation (absorption) • seismic wave propagation is not completely elastic • small fraction of seismic energy is converted to frictional heat • loss of energy = decrease in amplitude • characterize this with the “quality factor” (Q): ! ! ! 2πE Q= ΔE • Q is a measure of the fractional loss of energy per cycle (oscillation) of the seismic wave • high Q mean little energy loss • can show that the loss of energy will cause an exponential decrease in seismic wave amplitude over time (t): ! ! A( t ) = A 0 e − πft Q (e is the exponential constant 2.718) • note that this is a function of frequency • higher frequency = more cycles per second = more energy lost • can also write in terms of distance traveled by wave (x): ! ! ! à A( x ) = A 0 e − πx Qλ amplitude decays more rapidly for: low Q or high f (short λ) (Material) (Seismic wave) Example of attenuation: Common approach to calculate Q Interpretation 1: Suppose A0 represents wave amplitude, then A = A0e−bt = A0e−ω 0 t /(2Q ) ln(A) $ω 0 ' ln(A) = ln(A0 ) − & )t %2Q( € intercept slope t € Star Track ! The Q )37 The Earth is more attenuating than the Moon. ! Problem: where are P, S, Surf. waves? )38 • seismic sources release energy over a wide range of frequencies (Kearey et al., 2002) • as wave travels, the high frequency components will be more strongly attenuated • over time, wave is dominated by low frequency (long wavelength) components à seismic wave will become smoother and more spread out over time (similar to thunder) • for crustal rocks, Q is typically 100-200 • QP > QS à energy loss caused mostly by shear deformation 3. Scattering • most materials contain small heterogeneities • grains, mineral boundaries, pore edges, cracks, etc. • some seismic energy is scattered when it encounters these features • therefore amplitude will decrease Wavelength effect demonstrated for P wave coda. People use source spectrum to analyze the coda and obtain information about Q and scatters about a given path