Quantum Theory 1 - Home Exercise 9
... (a) Calculate the differential form of L̂+ and L̂− . (b) Use a direct calculation(integrals over wavefunctions etc.) to calculate the matrix representations of the following operators given that l = 2. i. L̂x ii. L̂y iii. L̂z iv. L̂+ v. L̂− vi. L̂2 (c) Repeat the calculation using raising and loweri ...
... (a) Calculate the differential form of L̂+ and L̂− . (b) Use a direct calculation(integrals over wavefunctions etc.) to calculate the matrix representations of the following operators given that l = 2. i. L̂x ii. L̂y iii. L̂z iv. L̂+ v. L̂− vi. L̂2 (c) Repeat the calculation using raising and loweri ...
Quantum physics I
... •Each photon should have a definite value at all angles, whether measured or not; since QT doesn’t account for this attribute, it’s incomplete ...
... •Each photon should have a definite value at all angles, whether measured or not; since QT doesn’t account for this attribute, it’s incomplete ...
5.11 Harmonic Oscillator
... Particle in well – how to solve the SE – energy levels – quantization – expectation values – effect of well length – effect of well height – calculating probabilities – compare and contrast with infinite well – classically forbidden ...
... Particle in well – how to solve the SE – energy levels – quantization – expectation values – effect of well length – effect of well height – calculating probabilities – compare and contrast with infinite well – classically forbidden ...
Homework 2
... (a) Determine the effective potential for the motion of the electron around the nucleus as a function of the radial distance. (b) According to the Bohr model, electrons move on circular orbits and the angular momentum L can assume the values L = n~, n ∈ {1, 2, . . .}. Determine the possible energies ...
... (a) Determine the effective potential for the motion of the electron around the nucleus as a function of the radial distance. (b) According to the Bohr model, electrons move on circular orbits and the angular momentum L can assume the values L = n~, n ∈ {1, 2, . . .}. Determine the possible energies ...
Homework No. 01 (Spring 2016) PHYS 530A: Quantum Mechanics II
... (a) Find the Lagrangian for this system that implies the equation of motion of Eq. (1) using Hamilton’s principle of stationary action. (b) Determine the canonical momentum for this system (c) Determine the Hamilton H(p, x) for this system. 2. (10 points.) The Hamiltonian is defined by the relation ...
... (a) Find the Lagrangian for this system that implies the equation of motion of Eq. (1) using Hamilton’s principle of stationary action. (b) Determine the canonical momentum for this system (c) Determine the Hamilton H(p, x) for this system. 2. (10 points.) The Hamiltonian is defined by the relation ...
Theoretical Nonlinear and Quantum Optics Ray
... Department of Physics, National TsingHua University, Hsinchu, Taiwan Institute of Photonics Technologies, National TsingHua University, Hsinchu, Taiwan * [email protected] Counter-intuitive pictures of waves are predicted both in the classical and quantum worlds. In contrast to the wellknown circ ...
... Department of Physics, National TsingHua University, Hsinchu, Taiwan Institute of Photonics Technologies, National TsingHua University, Hsinchu, Taiwan * [email protected] Counter-intuitive pictures of waves are predicted both in the classical and quantum worlds. In contrast to the wellknown circ ...
My Century of Physics
... is very intuitive as follows: the elementary particles are knotted current loops of energymomentum in the sense of SLq(2), i.e. with the topological quantum numbers (j, m, m0 ) determined by ...
... is very intuitive as follows: the elementary particles are knotted current loops of energymomentum in the sense of SLq(2), i.e. with the topological quantum numbers (j, m, m0 ) determined by ...
pdf - inst.eecs.berkeley.edu
... complex vector space. They may be degenerate, i.e., several having the same value. The set {ai } is called the “spectrum” of Â. • the eigenvalues are the roots of the secular equation det(A − aI) = 0, i.e., the roots of an algebraic equation of degree d. • the basis vectors |1i, |2i, ...|di that di ...
... complex vector space. They may be degenerate, i.e., several having the same value. The set {ai } is called the “spectrum” of Â. • the eigenvalues are the roots of the secular equation det(A − aI) = 0, i.e., the roots of an algebraic equation of degree d. • the basis vectors |1i, |2i, ...|di that di ...
(pdf)
... L : X × V → R. Then through the Legendre transform, the Hamiltonian is a functional H : X × V ∗ → R. Let Z be a Banach space, which we call a state space. The state space of classical mechanics is Z = R3 × R3 , whereas the Klein-Gordon state space is Z = H 1 (Rd ) × L2 (Rd ). Now that we have determ ...
... L : X × V → R. Then through the Legendre transform, the Hamiltonian is a functional H : X × V ∗ → R. Let Z be a Banach space, which we call a state space. The state space of classical mechanics is Z = R3 × R3 , whereas the Klein-Gordon state space is Z = H 1 (Rd ) × L2 (Rd ). Now that we have determ ...
Particles & Strings - University of Southampton
... Quantum Gravity If the vacuum is full of all this stuff shouldn’t we be pulled gravitationally by it? Since it is uniformily distributed there is no net pull (equal space to all sides) But General Relativity says the energy should uniformily curve space-time… the Universe should be the size of a gr ...
... Quantum Gravity If the vacuum is full of all this stuff shouldn’t we be pulled gravitationally by it? Since it is uniformily distributed there is no net pull (equal space to all sides) But General Relativity says the energy should uniformily curve space-time… the Universe should be the size of a gr ...
Quantum Computing
... The (seeming) impossibility of the first two machines reflects fundamental principles of physics—Special Relativity and the Second Law respectively So what about the third one? ...
... The (seeming) impossibility of the first two machines reflects fundamental principles of physics—Special Relativity and the Second Law respectively So what about the third one? ...
Quantum back-reaction and the particle law of motion
... and find a physical basis for adopting the de Broglie-Bohm law. Here we attempt to develop an alternative method suggested by consideration of the dynamical implications and consistency of one of the most distinctive aspects of the de Broglie-Bohm theory: that, in acting on the particle, the guiding ...
... and find a physical basis for adopting the de Broglie-Bohm law. Here we attempt to develop an alternative method suggested by consideration of the dynamical implications and consistency of one of the most distinctive aspects of the de Broglie-Bohm theory: that, in acting on the particle, the guiding ...
485-organizational-meeting-Fall
... However, attempts to describe atomic particles as point masses governed by the laws of classical mechanics and field theory (E&M) fail for an increasing set of experimental observations. ...
... However, attempts to describe atomic particles as point masses governed by the laws of classical mechanics and field theory (E&M) fail for an increasing set of experimental observations. ...
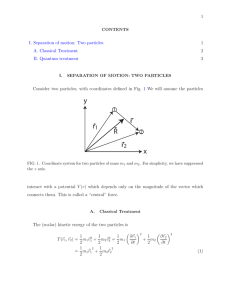
Separation of internal and center-of
... Consider two particles, with coordinates defined in Fig. 1 We will assume the particles ...
... Consider two particles, with coordinates defined in Fig. 1 We will assume the particles ...
The Origin of Inertia
... interpretation of mass-energy. However one has to be careful to maintain self-consistency when comparing theoretical models. The quantum vacuum-inertia concept implies -- via the principle of equivalence -- that gravitation must also have a connection to the ZPF (along lines conjectured by Sakharov ...
... interpretation of mass-energy. However one has to be careful to maintain self-consistency when comparing theoretical models. The quantum vacuum-inertia concept implies -- via the principle of equivalence -- that gravitation must also have a connection to the ZPF (along lines conjectured by Sakharov ...