Polygon
... • About Our Trip……Polygons are all around us in our everyday lives. They are on buildings, road signs, playgrounds, and even in the classroom! We are going to travel the world looking for polygons in real life situations. • A polygon is a two dimensional shape that is closed and made with straight ...
... • About Our Trip……Polygons are all around us in our everyday lives. They are on buildings, road signs, playgrounds, and even in the classroom! We are going to travel the world looking for polygons in real life situations. • A polygon is a two dimensional shape that is closed and made with straight ...
UNIT 5e GEOMETRY
... student draws two lines that intersect. Measure the length of each line to the nearest millimetre and one of the angles to the nearest degree. Each student should then measure another student’s drawing and compare answers. Show how to: construct a triangle using a ruler and compasses only, given the ...
... student draws two lines that intersect. Measure the length of each line to the nearest millimetre and one of the angles to the nearest degree. Each student should then measure another student’s drawing and compare answers. Show how to: construct a triangle using a ruler and compasses only, given the ...
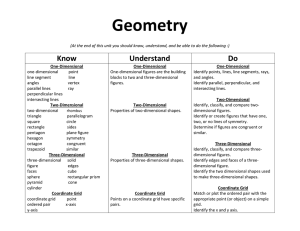
Geometry
... Geometry Key Learning: Geometric figures and relationships can be classified by characteristics. Unit Essential Question: How are geometric figures classified? ...
... Geometry Key Learning: Geometric figures and relationships can be classified by characteristics. Unit Essential Question: How are geometric figures classified? ...
UNIT 5e GEOMETRY
... and angles through various exercises. For example, each student draws two lines that intersect. Measure the length of each line to the nearest millimetre and one of the angles to the nearest degree. Each student should then measure another student’s drawing and compare answers. Show how to: construc ...
... and angles through various exercises. For example, each student draws two lines that intersect. Measure the length of each line to the nearest millimetre and one of the angles to the nearest degree. Each student should then measure another student’s drawing and compare answers. Show how to: construc ...
Two Dimensional Areas Crossword
... The distance from the center of a regular polygon to any one of its vertices is called the _____. The ratio of a circle's circumference to its diameter is represented by the Greek letter ____. The oblique parallelogram has the same area as a(n) _____ with the same base and height--but not the same p ...
... The distance from the center of a regular polygon to any one of its vertices is called the _____. The ratio of a circle's circumference to its diameter is represented by the Greek letter ____. The oblique parallelogram has the same area as a(n) _____ with the same base and height--but not the same p ...
Geometric Shapes
... Geometric shapes are found in the design of most products and structures. Some are more obvious than others. You can look around you and identify a geometric shape. One of the most common types of geometric shapes is the rectangle, a rectangle can be found in almost every feature of a residential ho ...
... Geometric shapes are found in the design of most products and structures. Some are more obvious than others. You can look around you and identify a geometric shape. One of the most common types of geometric shapes is the rectangle, a rectangle can be found in almost every feature of a residential ho ...
4-6-int-ext-angles
... How can we figure out how much each interior angle is in a regular polygon? Consider the regular pentagon to the right: (a) What is the least number of degrees the pentagon can be rotated to that it is mapped back onto itself? ...
... How can we figure out how much each interior angle is in a regular polygon? Consider the regular pentagon to the right: (a) What is the least number of degrees the pentagon can be rotated to that it is mapped back onto itself? ...
QUESTIONS for latest set of presentations
... c. The Law of Large Numbers d. Theory of Probabilities 4. The first comprehensive book on statistics and probability was published in 1713 and written by whom? a. Jakob Bernoulli b. Johann Bernoulli c. John Graunt d. William Petty 5. Statistics is still considered to be a branch of mathematics. 6. W ...
... c. The Law of Large Numbers d. Theory of Probabilities 4. The first comprehensive book on statistics and probability was published in 1713 and written by whom? a. Jakob Bernoulli b. Johann Bernoulli c. John Graunt d. William Petty 5. Statistics is still considered to be a branch of mathematics. 6. W ...
geometry - Blount County Schools
... angles formed by parallel and perpendicular lines, vertical angles, adjacent angles, complementary angles, and supplementary angles. ...
... angles formed by parallel and perpendicular lines, vertical angles, adjacent angles, complementary angles, and supplementary angles. ...
3-D Figures
... points. Draw the figure’s edges along the sight lines. 4. Within the sight lines draw the rest of the vertical edges parallel to the front edge. 5. Connect all vertices with both vanishing points. Draw the remaining edges of the figure. Three Point Perspective – all parallel lines meet at a vanishin ...
... points. Draw the figure’s edges along the sight lines. 4. Within the sight lines draw the rest of the vertical edges parallel to the front edge. 5. Connect all vertices with both vanishing points. Draw the remaining edges of the figure. Three Point Perspective – all parallel lines meet at a vanishin ...
Construction 12: Construct a circle circumscribed about a triangle. 1
... points. Draw the figure’s edges along the sight lines. 4. Within the sight lines draw the rest of the vertical edges parallel to the front edge. 5. Connect all vertices with both vanishing points. Draw the remaining edges of the figure. Three Point Perspective – all parallel lines meet at a vanishin ...
... points. Draw the figure’s edges along the sight lines. 4. Within the sight lines draw the rest of the vertical edges parallel to the front edge. 5. Connect all vertices with both vanishing points. Draw the remaining edges of the figure. Three Point Perspective – all parallel lines meet at a vanishin ...
Section 6.1 Similar Figures
... polygons If two polygons are similar, then the ratio of their perimeters is equal to the ratio of their corresponding side lengths. Corresponding lengths in similar polygons: If two polygons are similar, then the ratio of any two corresponding lengths in the polygons is equal to the scale factor of ...
... polygons If two polygons are similar, then the ratio of their perimeters is equal to the ratio of their corresponding side lengths. Corresponding lengths in similar polygons: If two polygons are similar, then the ratio of any two corresponding lengths in the polygons is equal to the scale factor of ...
Lecture 7
... with internal angle equal to α if and only if α ∈ [0, (n − 2)π/n). (Hint: Work in the Poincaré disc D. Let ω = e 2πi/n be an nth root of unity. Fix r ∈ (0, 1) and consider the polygon D(r) with vertices at r, rω, rω 2 , . . . , rω n−1 . This is a regular n-gon (why?). Let α(r) denote the internal a ...
... with internal angle equal to α if and only if α ∈ [0, (n − 2)π/n). (Hint: Work in the Poincaré disc D. Let ω = e 2πi/n be an nth root of unity. Fix r ∈ (0, 1) and consider the polygon D(r) with vertices at r, rω, rω 2 , . . . , rω n−1 . This is a regular n-gon (why?). Let α(r) denote the internal a ...
Regular polytope
In mathematics, a regular polytope is a polytope whose symmetry is transitive on its flags, thus giving it the highest degree of symmetry. All its elements or j-faces (for all 0 ≤ j ≤ n, where n is the dimension of the polytope) — cells, faces and so on — are also transitive on the symmetries of the polytope, and are regular polytopes of dimension ≤ n. Regular polytopes are the generalized analog in any number of dimensions of regular polygons (for example, the square or the regular pentagon) and regular polyhedra (for example, the cube). The strong symmetry of the regular polytopes gives them an aesthetic quality that interests both non-mathematicians and mathematicians.Classically, a regular polytope in n dimensions may be defined as having regular facets [(n − 1)-faces] and regular vertex figures. These two conditions are sufficient to ensure that all faces are alike and all vertices are alike. Note, however, that this definition does not work for abstract polytopes.A regular polytope can be represented by a Schläfli symbol of the form {a, b, c, ...., y, z}, with regular facets as {a, b, c, ..., y}, and regular vertex figures as {b, c, ..., y, z}.