Magical Monday - teresajpeterson
... 2.144= -12(x-5) x= -17 3.x-1 = 5x+3x-8 x= 1 4.2(4x-3) -8 = 4+2x x=3 ...
... 2.144= -12(x-5) x= -17 3.x-1 = 5x+3x-8 x= 1 4.2(4x-3) -8 = 4+2x x=3 ...
File
... sides where opposite sides are parallel. Also: • opposite sides are equal in length • and opposite angles are equal (angles "a" are the same, and angles "b" are the same) ...
... sides where opposite sides are parallel. Also: • opposite sides are equal in length • and opposite angles are equal (angles "a" are the same, and angles "b" are the same) ...
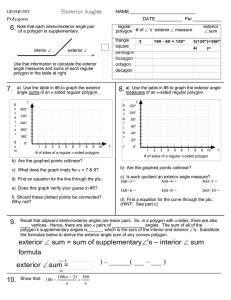
7.5 Angle Relationships in Polygons
... 2) Use the fact that an interior angle and its corresponding exterior angle are supplementary angles to determine the values of the exterior angles. ...
... 2) Use the fact that an interior angle and its corresponding exterior angle are supplementary angles to determine the values of the exterior angles. ...
Unit 4 - Brunswick School Department
... Lines, Line Segments, Rays, & Angles: Ray: A 2-dimensional figure that has one endpoint and goes without end in one direction. A ray is shown with an endpoint and an arrow at one end. Line: A straight path that goes in two directions without end (forever and ever). The line will have arrows on both ...
... Lines, Line Segments, Rays, & Angles: Ray: A 2-dimensional figure that has one endpoint and goes without end in one direction. A ray is shown with an endpoint and an arrow at one end. Line: A straight path that goes in two directions without end (forever and ever). The line will have arrows on both ...
Geometry Chapter 7 Math Notes Parts of a Circle A circle is the set of
... and the same size. This means that if you know two triangles are congruent, you can state that corresponding parts are congruent. This can be also stated with the arrow diagram: ≅ Δs → ≅ parts For example, if ΔABC ≅ ΔPQR , then it follows that ∠A ≅∠P, ∠B ≅∠Q, and ∠C ≅∠R. Also, ...
... and the same size. This means that if you know two triangles are congruent, you can state that corresponding parts are congruent. This can be also stated with the arrow diagram: ≅ Δs → ≅ parts For example, if ΔABC ≅ ΔPQR , then it follows that ∠A ≅∠P, ∠B ≅∠Q, and ∠C ≅∠R. Also, ...
6. 8. exterior ∠ sum = sum of supplementary∠`s – interior ∠ sum
... Recall that adjacent interior/exterior angles are linear pairs. So, in a polygon with n-sides, there are also ____ vertices. Hence, there are also n pairs of _____________ angles. The sum of all of the polygon’s supplementary angles is______, which is the sum of the interior and exterior ∠’s. Substi ...
... Recall that adjacent interior/exterior angles are linear pairs. So, in a polygon with n-sides, there are also ____ vertices. Hence, there are also n pairs of _____________ angles. The sum of all of the polygon’s supplementary angles is______, which is the sum of the interior and exterior ∠’s. Substi ...
Similar Polygons Notes and Practice
... 5. If ABCD ∼ PQRS, find the scale factor of ABCD to PQRS and the perimeter of each polygon. ...
... 5. If ABCD ∼ PQRS, find the scale factor of ABCD to PQRS and the perimeter of each polygon. ...
Interior Angles of a Polygon
... So, each time we add a side (triangle to quadrilateral, quadrilateral to pentagon, etc), we add another 180° to the total: If it is a Regular Polygon.. ...
... So, each time we add a side (triangle to quadrilateral, quadrilateral to pentagon, etc), we add another 180° to the total: If it is a Regular Polygon.. ...
Analytical Calculation of Geodesic Lengths and Angle Measures on
... this paper we show how to use analytical methods to calculate the lengths of the geodesics and the measures of the angles for these tilings. ...
... this paper we show how to use analytical methods to calculate the lengths of the geodesics and the measures of the angles for these tilings. ...
Geometry
... Warm Up The geometric mean of 12 and another number is 30. What is the other number? ...
... Warm Up The geometric mean of 12 and another number is 30. What is the other number? ...
Geometry 1-6 9-2
... Mathematical Practices 2 Reason abstractly and quantitatively. 6 Attend to precision. ...
... Mathematical Practices 2 Reason abstractly and quantitatively. 6 Attend to precision. ...
Angles and Constructions
... 5” may be written as expressions involving “τ ” by using the relationship 5 = 2τ − 1. ...
... 5” may be written as expressions involving “τ ” by using the relationship 5 = 2τ − 1. ...
Made-to-Order Polygons
... help. Harry needs to color all the regular polygons using the color code above. Help Harry locate and color each regular polygon in the wall below. Remember that a regular polygon is a polygon with all sides the same length and all angles the same measure. ...
... help. Harry needs to color all the regular polygons using the color code above. Help Harry locate and color each regular polygon in the wall below. Remember that a regular polygon is a polygon with all sides the same length and all angles the same measure. ...
Week 8 Vocab - Heritage High School Math Department
... A solid shape with one curved surface and two congruent circular or elliptical bases A solid object that has two identical ends and all flat sides. The cross section is the same all along its length. The shape of the ends give the prism a name, such as "triangular prism" A solid shape with a polygon ...
... A solid shape with one curved surface and two congruent circular or elliptical bases A solid object that has two identical ends and all flat sides. The cross section is the same all along its length. The shape of the ends give the prism a name, such as "triangular prism" A solid shape with a polygon ...
Regular polytope
In mathematics, a regular polytope is a polytope whose symmetry is transitive on its flags, thus giving it the highest degree of symmetry. All its elements or j-faces (for all 0 ≤ j ≤ n, where n is the dimension of the polytope) — cells, faces and so on — are also transitive on the symmetries of the polytope, and are regular polytopes of dimension ≤ n. Regular polytopes are the generalized analog in any number of dimensions of regular polygons (for example, the square or the regular pentagon) and regular polyhedra (for example, the cube). The strong symmetry of the regular polytopes gives them an aesthetic quality that interests both non-mathematicians and mathematicians.Classically, a regular polytope in n dimensions may be defined as having regular facets [(n − 1)-faces] and regular vertex figures. These two conditions are sufficient to ensure that all faces are alike and all vertices are alike. Note, however, that this definition does not work for abstract polytopes.A regular polytope can be represented by a Schläfli symbol of the form {a, b, c, ...., y, z}, with regular facets as {a, b, c, ..., y}, and regular vertex figures as {b, c, ..., y, z}.