Download 2.5 - schsgeometry

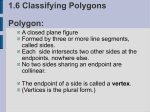
2.6
How Can Build It?
Pg. 19
Pinwheels and Polygons
2.6 – How Can I Build It?______________
Pinwheels and Polygons
In this section you will discover the
names of the many different polygons
and how they are classified.
2.30 – PINWHEELS AND POLYGONS
Itzel loves pinwheels. One day in class,
she noticed that if she put three
congruent triangles together, that one set
of the corresponding angles are adjacent,
she could make a shape that looks like a
pinwheel.
a. Can you determine any of the angles of
her triangles? Explain how you found
your answer.
360
3
120°
120°120°
b. The overall shape (outline) of Itzel's
pinwheel is shown at right. How many
sides does it have? What is another
name for this shape?
1
6 sides
hexagon
2
6
120°
120°120°
4
5
3
c. Itzel's shape is an example of a
polygon because it is a closed, two
dimensional figure made of straight line
segments connected end-to-end. As you
study polygons in this course, it is useful
to use these names because they identify
how many sides a particular polygon has.
Some of these words may be familiar,
while others may be new. Fill in the
names of the polygons below. Then,
draw an example of a heptagon.
Name of Polygon
# of sides
triangle
quadrilateral
pentagon
hexagon
3
heptagon
7
4
5
6
Name of Polygon
# of sides
octagon
nonagon
decagon
dodecagon
8
n – gon
9
10
12
n
Then, draw an example of a heptagon.
2.31 – MAKING PINWHEELS
Itzel is very excited. She wants to know if
you can build a pinwheel using any angle
of her triangle. Obtain a set of triangles
from your teacher. Work with your team to
build pinwheels and polygons by placing
different corresponding angles together at
the center. You will need to use the
triangles from all four team members
together to build one shape. Be ready to
share your results with the class.
3 triangles
120°
1
1
1
Angle #
1
2
3
# of triangles Measure of the
needed
central angle
3
120°
9 triangles
40°
Angle #
# of triangles Measure of the
needed
central angle
1
3
120°
2
9
40°
3
18 triangles
20°
Angle #
# of triangles Measure of the
needed
central angle
1
3
120°
2
9
18
40°
20°
3
2.32 –PINWHEEL PATTERNS
Jorge likes Itzel's pinwheels but
wonders, "Will all triangles build a
pinwheel or a polygon?”
a. Use the different triangles provided
by your teacher. Work together to
determine which congruent triangles
can build a pinwheel (or polygon) when
corresponding angles are placed
together at the center. If it works, fill in
the table.
Angle #
# of triangles
needed
Measure of the
central angle
A
8
45°
B
Not possible
C
5
D
Not possible
E
F
12
Not possible
72°
30°
b. Explain why one triangle may be able to
create a pinwheel or polygon while another
triangle cannot.
It must divide by 360° evenly
c. Jorge has a triangle with interior angle
measures 32°, 40°, and 108°. Will this
triangle be able to form a pinwheel?
Explain? If so, at what angle?
Yes, the 40° divides in evenly
2.33 –POLYGONS
Jasmine wants to create a pinwheel with
equilateral triangles.
a. How many equilateral triangles will she
need? Explain how you know.
60°
60° 60°
60° 60°
60°
360
60
6
b. What is the name for the polygon she
created?
hexagon
60°
60° 60°
60° 60°
60°
c. Jasmine's shape is an example of a
convex polygon, while Inez's shape, shown
at right is non-convex (or concave). Study
the examples below and write a definition of
a convex polygon on your paper.
Has vertices
going inward, like
a cave
All vertices point
outward
2.34 –CONCAVE VS. CONVEX
Brenda noticed that the non-convex
(concave) shapes all had a part that went
inward, like a cave. She decided to
investigate more. Sort the shapes below as
either "convex" or "concave".
convex
concave
convex
concave
2.35 –EQULATERAL, EQUIANGLUAR, AND
REGULAR
Brenda was curious about the relationship
between the sides and angles of polygons.
When all sides are equal, it is called
equilateral. When all angles are equal, the
polygon is called equiangular. When it has
all equal sides AND all equal angles it is
called regular.
Classify the name of the polygon by the
number of sides. Is the polygon equilateral,
equiangular, or regular? Then determine if
it is convex or concave.
hexagon
Name: _______________
Equilateral, Equiangular, Regular
Convex OR Concave
pentagon
Name: _______________
Equilateral, Equiangular, Regular
Convex OR Concave
octagon
Name: _______________
Equilateral, Equiangular, Regular
Convex OR Concave
decagon
Name: _______________
Equilateral, Equiangular, Regular
Convex OR Concave
heptagon
Name: _______________
Equilateral, Equiangular, Regular
Convex OR Concave
Name: quadrilateral
_______________
Equilateral, Equiangular, Regular
Convex OR Concave