(Greater than 90 degrees)
... b) The related acute angle β can be used as part of a right triangle with sides of 3 and 4. We can figure out β using SOHCAHTOA. Sin ...
... b) The related acute angle β can be used as part of a right triangle with sides of 3 and 4. We can figure out β using SOHCAHTOA. Sin ...
MT218:Layout 1
... aim to make students think about different partitions of a shape, and possibly work with fractions and irrational numbers. It will depend on the unit chosen to measure: length of the initial squared piece of paper versus length of the side of the small square that it is obtained when the initial squ ...
... aim to make students think about different partitions of a shape, and possibly work with fractions and irrational numbers. It will depend on the unit chosen to measure: length of the initial squared piece of paper versus length of the side of the small square that it is obtained when the initial squ ...
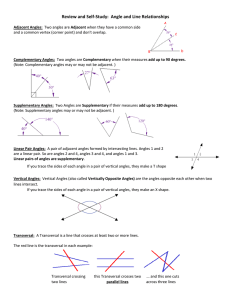
Review and Self-Study: Angle and Line Relationships
... If you trace the sides of each angle in a pair of vertical angles, they make a T shape Vertical Angles: Vertical Angles (also called Vertically Opposite Angles) are the angles opposite each other when two lines intersect. If you trace the sides of each angle in a pair of vertical angles, they make a ...
... If you trace the sides of each angle in a pair of vertical angles, they make a T shape Vertical Angles: Vertical Angles (also called Vertically Opposite Angles) are the angles opposite each other when two lines intersect. If you trace the sides of each angle in a pair of vertical angles, they make a ...
Unit descriptions
... Enduring Understanding: (1) Explore definitions, properties, and attributes of 2 and 3 dimensional objects. (2) To study conceptual issues of length, area, and volume and their complex interrelationships Essential Questions: (1) Can the student find the surface area and volume of 3- dimensional shap ...
... Enduring Understanding: (1) Explore definitions, properties, and attributes of 2 and 3 dimensional objects. (2) To study conceptual issues of length, area, and volume and their complex interrelationships Essential Questions: (1) Can the student find the surface area and volume of 3- dimensional shap ...
Congruent shapes Congruent shapes have the same size and the
... Congruent shapes have the same size and the same shape. In other words, if you place an object in front of a mirror, the image that you see is congruent or " equal " to the object When shapes are congruent, all corresponding sides and angles are also congruent. Look at the following two triangles.Yo ...
... Congruent shapes have the same size and the same shape. In other words, if you place an object in front of a mirror, the image that you see is congruent or " equal " to the object When shapes are congruent, all corresponding sides and angles are also congruent. Look at the following two triangles.Yo ...
HS_LTMR_02 Angle_Measure_v2
... 1) Complementary angles are two angles whose measures add up to 2) Supplementary angles are two angles whose measures add up to 3) The sum of the interior measures of any triangle is degrees. ...
... 1) Complementary angles are two angles whose measures add up to 2) Supplementary angles are two angles whose measures add up to 3) The sum of the interior measures of any triangle is degrees. ...