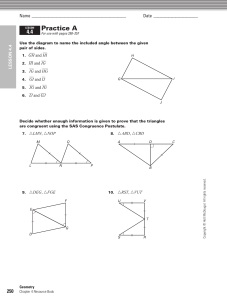
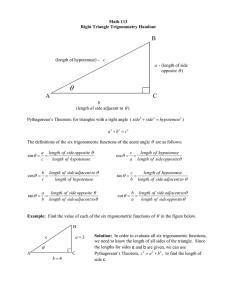
Grade 6 Math Circles Angles Introduction Review: Types of Angles
... Corresponding angles are angles that are on the same side of the transversal, and on matching sides of their own line. When the lines are parallel, corresponding angles are congruent. In the diagram above, a and e are corresponding angles, b and f are corresponding angles, c and g are corresponding ...
... Corresponding angles are angles that are on the same side of the transversal, and on matching sides of their own line. When the lines are parallel, corresponding angles are congruent. In the diagram above, a and e are corresponding angles, b and f are corresponding angles, c and g are corresponding ...
VECTOR ALGEBRA IMPORTANT POINTS TO REMEMBER A
... 5. A vector has length 21 and d. r.s 2, -3, 6. Find the direction cosines and components of , given that it makes an acute angle with x axis. 6. Find the angles at which the vector 2 - + 2 is inclined to each of the coordinate axes. 7. For any vector , prove that = ( . ) + ( . ) + ( . ) . 8. Find th ...
... 5. A vector has length 21 and d. r.s 2, -3, 6. Find the direction cosines and components of , given that it makes an acute angle with x axis. 6. Find the angles at which the vector 2 - + 2 is inclined to each of the coordinate axes. 7. For any vector , prove that = ( . ) + ( . ) + ( . ) . 8. Find th ...
Chapter 5: Poincare Models of Hyperbolic Geometry
... −M followed by inversion in the unit circle. This map ϕ is an isometry because it is the composition of two isometries. Note that M is first sent to O and then to ∞ by inversion. Thus, the image of Γ is a (Euclidean) line. Since the center of the circle is on the real axis, the circle intersects the ...
... −M followed by inversion in the unit circle. This map ϕ is an isometry because it is the composition of two isometries. Note that M is first sent to O and then to ∞ by inversion. Thus, the image of Γ is a (Euclidean) line. Since the center of the circle is on the real axis, the circle intersects the ...
Math 90 Unit 8 – Circle Geometry
... 8.1 – Properties of Tangents to a Circle Investigate: Page 384 A line that intersects a circle at only one point is a tangent to the circle. The point where the tangent intersects the circle is the point of tangency. For example: Line AB is a tangent to the circle with center O. Point P is the point ...
... 8.1 – Properties of Tangents to a Circle Investigate: Page 384 A line that intersects a circle at only one point is a tangent to the circle. The point where the tangent intersects the circle is the point of tangency. For example: Line AB is a tangent to the circle with center O. Point P is the point ...