Download Law of Sines

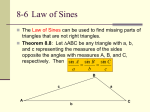
Module 6 Lesson 1
Solving Triangles using the Law of Sines – Part 1
We spent time in module 4 solving triangles, which were all right triangles. Now we
learn what to do if the triangles we’re considering are NOT right triangles.
Example 1: Solve this triangle:
a  15 cm, A  25 , C  100
In the last module, you solved many triangles but they were all right triangles. We don’t
have a right triangle in this example. Let’s sketch our picture:
The above picture is not drawn to scale. The important thing is that side “a” is opposite
Angle A, side “b” is opposite Angle B, and side “c” is opposite Angle C.
Finding Angle B should be fairly easy. Once again, all three angles of the triangle need
to add up to 180°. Simply subtract:
180 -100 - 25 = 55
B  55
Now, we address the more difficult problem of finding the missing sides. The three trig
functions (sine, cosine, tangent) and methods we learned previously only apply to right
triangles. We need something new to help us with this problem:
1
Law of Sines
That new helpful tool is called the Law of Sines. The Law of Sines applies to all triangles
(including right triangles). Here it is:
a
b
c


sin A sin B sin C
Law of Sines:
The law states that the ratio between each side length and the sine of its opposite angle
is the same for each side/angle combination in the triangle.
Note that there are three sections to the Law of Sines. We use only two of those
sections at one time. Let’s look back at our example. We have Angle A, Angle C and
side “a” given to us. We can therefore use the Law of Sines like this:
a
c

sin A sin C
Put in your values but be warned! The place where most students miss these problems
is that they forget to put sin on the bottom of the fraction along with the angle. They
simply put the angle measure. Don’t make this mistake:
RIGHT:
15
c

sin 25 sin100
WRONG:
15
c

25 100
We have a proportion, so we cross-multiply to solve:
15
c
=
sin 25 sin100
15 × sin100 = c ×sin 25
Divide each side by sin 25 :
15 × sin100 c × sin 25
=
sin 25
sin 25
15 × sin100
=c
sin 25
We’ve now solved for “c ”. Use your calculator and close your parenthesis around the
numerator!!! This is second most popular place that students make mistakes on this
problem. They don’t close their parentheses.
You should get c
»
35.0 cm
2
Is your answer reasonable? 100 degrees is bigger than 25 degrees, so our answer
should be longer than 15 cm.
b
c
a
b
=

Now let’s find “b”. Should we use:
or
sin B sinC
sin A sin B
Does it matter?
Either ratio will lead you to find “b” however, we found “c ” and angle “B” through the
our calculations, make sure you didn’t make any mistakes in the calculations before you
use either “c” or “B.”
Example 1 continued
a
b
=
sin A sin B
15
b
=
sin 25 sin55
15 × sin55 = b × sin 25
15 × sin55 b × sin 25
=
sin 25
sin 25
15 × sin55
=b
sin 25
29.1 cm = b
or
b
c
=
sin B sin C
b
35
=
sin55 sin100
35 × sin55 = b × sin100
35 × sin55 b × sin100
=
sin100
sin100
35 × sin55
=b
sin100
29.1 cm = b
Our solution is: b » 29.1 cm, c » 35 cm, B = 55
****Please note that we could have also solved this triangle by first calculating the
15
b
measurement of side “b” by using the ratio
and then use the value of
=
sin 25° sin 55°
“b” to find the measurement of “c ” using
c
29.1
=
sin100° sin55°
or
c
15
=
sin100° sin25°
3
Example 2:
Solve this triangle:
b  22 ft, A  40 , B  80
The first step you need to do is complete a sketch of the triangle and label what you are
given.
First I am going to solve for the missing angle
180° - 80° - 40° = 60° therefore Ð C = 60°
Next I am going to solve for "a" using the Law of Sines
Choose 2 ratios that you can use to solve for a missing piece
b
a
=
sin B sin A
Substitute what you know in the ratio
22
a
=
sin 80° sin 40°
Solve for the unknown piece my cross multiplying
22 ×sin 40° = asin 80°
Divide each side by sin 80°
22 sin 40° asin 80°
=
sin 80°
sin 80°
a » 14.4 ft
4
Next we are going to solve for the final side "c" by setting up another ratio
Choose 2 ratios that you can use to solve for a missing piece
b
c
=
sin B sinC
Substitute what you know in the ratio
22
c
=
sin 80° sin 60°
Solve for the unknown piece my cross multiplying
22 ×sin 60° = csin 80°
Divide each side by sin 80°
22 sin 60° csin 80°
=
sin 80°
sin 80°
c » 19.3 ft
Our solution is: C = 60°, a »14.4 ft, and c » 19.3 ft
Do you have to solve this triangle with these EXACT steps? Could you do the process
differently or use different ratios?
Different Situations with Triangles
There’s more to the Law of Sines that we’ll get to in the next set of notes. I’d like to talk
about something else first:
What information do you have when given a triangle to solve?
We know that you need to have three pieces of information (of a possible six) from a
triangle in order to be able to fill in the missing parts.
This is true. However, there’s a little more to it than that. The specific information you
have will help indicate which method you should use to solve the triangle.
5
Here are possible combinations of three pieces of information you could
be given:
What you are given
Two angles and the side
NOT in between them
(Angle Angle Side)
(AAS)
Diagram of Triangle
How do you solve for the missing pieces
1. Use the sum of the angles in a triangle add
to be 180° to solve for the remaining parts.
2. Use the Law of Sines
(You can complete these steps in reverse
order if you choose)
Two angles and the side
in between them
(Angle Side Angle) (ASA)
1. Use the sum of the angles in a triangle add
to be 180° to solve for the remaining parts.
2. Use the Law of Sines
Two sides and an angle
NOT in between them
(Side Side Angle) (SSA)
1. Check to see how many solutions the
triangle has (this is only done on the SSA
case)
2. Use the Law of Sines
3. Use the Law of Sines and the sum of the
angles in a triangle add to be 180° to solve
for the remaining parts.
Two sides and the angle
in between them
(Side Angle Side) (SAS)
1. Use Law of Cosines
2. Use the Law of Cosines finding the largest
angle first. Then use the sum of the angles in
a triangle add to be
180° to solve for the remaining parts
Three sides
(Side Side Side) (SSS)
1. Use the Law of Cosines.
2. Use the Law of Cosines finding the largest
angle first. Then use the sum of the angles in
a triangle add to be
180° to solve for the remaining parts
Three angles
(Angle Angle Angle
(AAA)
This triangle cannot be solved.
http://www.mathsisfun.com/algebra/trigsolving-triangles.html
6
In the 2 examples above we were given two angles and the side NOT in between them
(AAS).
As we move forward to look at the other combinations that we can be given, you need
to start recognizing which of these situations you have and which method you’ll use to
solve. Sometimes, you’ll use Law of Sines. Other times, you’ll start with the Law of
Cosines (Lesson 2). You’ll have to learn the different situations.
7