Download Name - Issaquah Connect

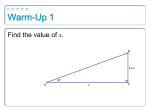
Name: __________________________________ Period _____ Right Triangle Trigonometry
Assignment: Section 12-1 #1-7, 11, 13, 14, and 16 Calculator Note: Use DEGREE MODE
Important Vocabulary you need to know:
(1) Corresponding Sides & Corresponding Angles of
Similar Triangles.
(2) Right Triangle
(3) Adjacent side to an angle
(4) Opposite side to an angle
(5) Hypotenuse the longest side in a right triangle
(6) Ratio is a fraction
Side a is opposite angle A
(7) Trigonometric Ratio: Sine, Cosine and Tangent
Side b is adjacent to angle B
Pythagorean Theorem: a 2  b 2  c 2
Similar Triangles: You’ve learned that corresponding sides of similar triangles have the same ratio.
The three triangles shown below are similar because all three corresponding angles are congruent.
The ratio of the length of the shorter
side to the length of the
middle-length side is always 0.75.
shortest leg 6 4.8 3
 
  0.75
middle leg 8 6.4 4
(1) Find the ratio of the length of the middle-length side to the longest side:
middle-length leg

longest leg


 ______
(2) Find the ratio of the length of the shortest side to the longest side:
shortest leg

longest leg


 ______
These ratios are called trigonometric ratios (abbreviated as “trig ratios”).
For any acute angle A in a right triangle, the three trig ratios are defined:
Opposite leg a

Hypotenuse c
Adjacent leg b
Cosine of A is a ratio: cos( A) 

Hypotenuse c
Opposite leg a
Tangent of A is a ratio: tan( A) 

Adjacent leg b
Sine of A is a ratio:
sin( A) 
Acute angles are A & B
(3) Write the Sine, Cosine and Tangent of angle B using the letters a, b, and c.
Sine of B is a ratio:
sin( B) 
Opposite leg

Hypotenuse
Cosine of B is a ratio:
cos( B) 
Adjacent leg

Hypotenuse
Tangent of B is a ratio: tan( B) 
Opposite leg

Adjacent leg
You can use the trig ratios to find an unknown side in a right triangle.
Example: Find the unknown length x in the triangle shown below.

Label the hypotenuse and the opposite & adjacent
sides to a known angle. (see diagram)

Write down the trig ratio you need to use.
Adjacent leg
Hypotenuse
cos( A) 

Fill in the numbers and solve for the unknown side.
cos(43) 

20
x
Solve for x.
( x) cos(43)  20
20
x
 27.35 cm
cos(43)
Hint:
You use the cosine ratio on
this example because you
know the adjacent side and
want to find the hypotenuse.
You try this one: Find the unknown length x in the triangle shown below.

Label the hypotenuse and the opposite & adjacent
sides to a known angle ON THE DIAGRAM

Write down the trig ratio you need to use.

Fill in the numbers and solve for the unknown side.
Solve for x.

Hint:
You use the sine ratio on this
example because you know the
opposite side and want to find the
hypotenuse.
You try this another one: Find the unknown length x

Label the hypotenuse and the opposite & adjacent
sides to a known angle ON THE DIAGRAM

Write down the trig ratio you need to use.

Fill in the numbers and solve for the unknown side.
Solve for x.

Hint:
You use the tangent ratio on this
example because you know the
adjacent side and want to find the
opposite.
You try this another one: Find the unknown length x

Label the hypotenuse and the opposite & adjacent
sides to a known angle ON THE DIAGRAM

Write down the trig ratio you need to use.

Fill in the numbers and solve for the unknown side.
Solve for x.

Hint:
You use the tangent ratio on this
example because you know the
opposite side and want to find the
adjacent.
You try this another one: Find the unknown length x

Label the hypotenuse and the opposite & adjacent
sides to a known angle ON THE DIAGRAM

Write down the trig ratio you need to use.

Fill in the numbers and solve for the unknown side.
Solve for x.

Hint:
You use the sine ratio on this
example because you know the
hypotenuse and want to find the
opposite side.
You can use the trig ratios to find an unknown angle in a right triangle.
Remember that the inverse function switches the x and y values.
That means if you have a trig ratio such as: y  cos( angle)
the inverse trig function would be angle  cos
1
1
To summarize: USE inverse trig functions ( cos , sin
1
y
A, tan 1 A ) to find an angles.
Example: Find the unknown angle x

Label the known sides as hypotenuse and adjacent to the
angle you are trying to find. (see the diagram)

Write down the trig ratio you need to use.
Adjacent leg
cos( A) 
Hypotenuse

Fill in the value for the sides that you know.
20
cos( x) 
75

Use the inverse cosine function to solve for the unknown
 20 
angle x:
x  cos 1  
 75 

Use your calculator to get an approximate answer.
 20 
x  cos 1    74.5 degrees
 75 
You try this one: Find the unknown angle x

Label the known sides as hypotenuse, adjacent or opposite
side to the angle you are trying to find
ON THE DIAGRAM.

Write down the trig ratio you need to use.

Fill in the value for the sides that you know.

Use the inverse trig function to solve for the unknown angle x:
Use your calculator to get an approximate answer.

Hint:
You use the cosine
ratio on this example
because you know the
adjacent side and the
hypotenuse.
Hint:
You use the tangent
ratio on this example
because you know the
opposite side and
adjacent side.
You try this one: Find the unknown angle x

Label the known sides as hypotenuse, adjacent or opposite
side to the angle you are trying to find
ON THE DIAGRAM.

Write down the trig ratio you need to use.

Fill in the value for the sides that you know.

Use the inverse trig function to solve for the unknown angle x:
Hint:
You use the sine ratio on
this example because
you know the opposite
side and hypotenuse.
Use your calculator to get an approximate answer.

When you are working with the trig ratios always draw the triangle and label the
sides as either: (1) opposite or (2) adjacent to an angle and the hypotenuse. If you
do this it will help you select the correct trig ratio to use.
Directions: Draw a right triangle for each problem.
Label the sides and angle, and then solve to find the unknown measure.
Example: cos(40 ) 
a
adjacent

20 hypotenuse
Draw a triangle: label hypotenuse & adjacent
You try: tan(40 ) 
b

5
Draw a triangle and label the diagram like the
example shown at the left.
Write the trig ratio and solve for the unknown side.
a
cos(40 ) 
20
a  20cos(40 )  15.3
Write the trig ratio and solve for the unknown side.
Example: Use trig ratios to solve problems.
Two hikers leave their campsite. Tom walks north 5.7 miles and Sam walks east 4.2 miles.
(a) After Tom gets to his destination, he looks directly toward Sam’s destination.
What is the measure of the angle between the path Tom walked and his line of sight to Sam’s
destination?
(b) How far apart are Sam and Tom?

Draw a right triangle using the given information.

Select the trig ratio you need to use and write in the numbers:
tan( A) 

Opposite 4.2

Adjacent 5.7
Use the inverse tangent function to solve for the angle.
 4.2 
A  tan 1 
  36.4 degrees
 5.7 

Use Pythagorean Theorem or
the sine or cosine ratio to solve for the distance, D.
sin(36.4) 
4.2
D
4.2
sin(36.4)
D  7.1 miles
D
cos(36.4) 
5.7
D
5.7
cos(36.4)
D  7.1 miles
D
( Sam) 2  (Tom) 2  D 2
(4.2) 2  (5.7) 2  D 2
50.13  D 2
D  50.13
D  7.1 miles
Answers:
(a) 36.4 degrees
(b) 7.1 miles
YOU TRY: Two hikers leave their campsite. Sue walks south 3.2 miles and Kate walks west 4.7 miles.
(a) After Sue gets to her destination, she looks directly toward Kate’s destination.
What is the measure of the angle between the path Sue walked and her line of sight to Kate’s
destination?
(b) How far apart are Sue and Kate?

Select the trig ratio you need to use and write in the numbers:
Draw a right triangle using the
given information.

Use the inverse tangent function to solve for the angle.
Use Pythagorean Theorem or the sine or cosine ratio to solve for
the distance, D.
Use sine ratio
Use cosine ratio
Use Pythagorean
Theorem
Answers:
(a) _________ degrees
(b) __________ miles