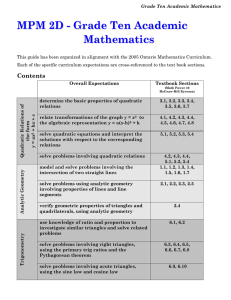
SSS, SAS, AAS, ASA
... Pythagorean Theorem By the end of this lesson, you should be able to 1. Determine if two right triangles are congruent. 2. Use the Pythagorean Theorem to solve problems. A few episodes ago, we looked at determining whether ANY two triangles were congruent. To review, there were several combinations ...
... Pythagorean Theorem By the end of this lesson, you should be able to 1. Determine if two right triangles are congruent. 2. Use the Pythagorean Theorem to solve problems. A few episodes ago, we looked at determining whether ANY two triangles were congruent. To review, there were several combinations ...
ExamReviewSheet.Dec2016INK
... What are the loci of points that are equidistant from two points, A and B and also equidistant from two parallel planes? The loci is the intersection of a plane which is equidistant from A and B and the perpendicular bisector of AB , and a plane which is between the parallel planes. This intersectio ...
... What are the loci of points that are equidistant from two points, A and B and also equidistant from two parallel planes? The loci is the intersection of a plane which is equidistant from A and B and the perpendicular bisector of AB , and a plane which is between the parallel planes. This intersectio ...
Document
... 4-4 Triangle Congruence: SSS and SAS For example, you only need to know that two triangles have three pairs of congruent corresponding sides. This can be expressed as the following postulate. ...
... 4-4 Triangle Congruence: SSS and SAS For example, you only need to know that two triangles have three pairs of congruent corresponding sides. This can be expressed as the following postulate. ...
4 Arithmetic of Segments—Hilbert`s Road from Ge
... In this section, we explain Hilbert’s procedure to construct an arithmetic of segments, also called Streckenrechnung. Hilbert constructs a field from a given model of geometry and thus opens up a quiet general road from geometry to algebra. The approach is explained in Hilbert’s foundations. It works ...
... In this section, we explain Hilbert’s procedure to construct an arithmetic of segments, also called Streckenrechnung. Hilbert constructs a field from a given model of geometry and thus opens up a quiet general road from geometry to algebra. The approach is explained in Hilbert’s foundations. It works ...
Chapter 6 Polygons and Quadrilaterals
... regularity, congruence, and similarity. G.4: Students identify and describe types of triangles. They identify and draw altitudes, medians, and angle bisectors. They use congruence and similarity. They find measures of sides, perimeters, and areas. They apply inequality theorems. G.4.1: Identify and ...
... regularity, congruence, and similarity. G.4: Students identify and describe types of triangles. They identify and draw altitudes, medians, and angle bisectors. They use congruence and similarity. They find measures of sides, perimeters, and areas. They apply inequality theorems. G.4.1: Identify and ...
Geometry
... Order Pairs: A pair of numbers where order is important, for example, (4,6) is different to (6,4). Often used to indicate on a coordinate plane, graph or map. Coordinate Plane: A plane containing two perpendicular axes (x and y) intersecting at a point called the origin (0,0). Two-Dimensional: A m ...
... Order Pairs: A pair of numbers where order is important, for example, (4,6) is different to (6,4). Often used to indicate on a coordinate plane, graph or map. Coordinate Plane: A plane containing two perpendicular axes (x and y) intersecting at a point called the origin (0,0). Two-Dimensional: A m ...
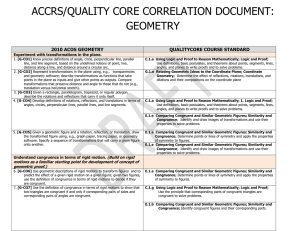
ACCRS/QualityCore-Geometry Correlation - UPDATED
... Use inductive reasoning to make conjectures and deductive reasoning to arrive at valid conclusions. D.1.b Identifying, Classifying, and Applying the Properties of Geometric Figures in Space; Points, Lines, Planes, and Space; Identify vertical, adjacent, complementary, and supplementary angle pairs a ...
... Use inductive reasoning to make conjectures and deductive reasoning to arrive at valid conclusions. D.1.b Identifying, Classifying, and Applying the Properties of Geometric Figures in Space; Points, Lines, Planes, and Space; Identify vertical, adjacent, complementary, and supplementary angle pairs a ...
History of geometry

Geometry (from the Ancient Greek: γεωμετρία; geo- ""earth"", -metron ""measurement"") arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers (arithmetic).Classic geometry was focused in compass and straightedge constructions. Geometry was revolutionized by Euclid, who introduced mathematical rigor and the axiomatic method still in use today. His book, The Elements is widely considered the most influential textbook of all time, and was known to all educated people in the West until the middle of the 20th century.In modern times, geometric concepts have been generalized to a high level of abstraction and complexity, and have been subjected to the methods of calculus and abstract algebra, so that many modern branches of the field are barely recognizable as the descendants of early geometry. (See Areas of mathematics and Algebraic geometry.)