Triangle Congruence and Similarity, v1
... emphasis on formalism is vastly more effective when students are a couple of years older. Therefore, I recommend that students have a lot of experience with interesting questions involving geometry (including but not limited to transformations) before being introduced to the ideas in this paper, whi ...
... emphasis on formalism is vastly more effective when students are a couple of years older. Therefore, I recommend that students have a lot of experience with interesting questions involving geometry (including but not limited to transformations) before being introduced to the ideas in this paper, whi ...
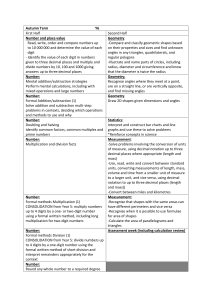
Review for Quizzes and Tests
... Lengths of sides that make a triangle Type of triangle – acute, obtuse, right Largest Side across from largest angle Exterior angle = sum of two remote interior angles Short cuts to prove triangles congruent and Congruency statement Problems will be similar to what you have done for homework problem ...
... Lengths of sides that make a triangle Type of triangle – acute, obtuse, right Largest Side across from largest angle Exterior angle = sum of two remote interior angles Short cuts to prove triangles congruent and Congruency statement Problems will be similar to what you have done for homework problem ...
The three classic problems of geometry
... so we can square the circle iff we can construct √π. A cube Q of side length 1 has volume 1; to double it, we’d need to construct a line segment of length 3 2. Finally, it turns out that trisecting an arbitrary angle is equivalent to being able to construct a root of a certain cubic equation. It tur ...
... so we can square the circle iff we can construct √π. A cube Q of side length 1 has volume 1; to double it, we’d need to construct a line segment of length 3 2. Finally, it turns out that trisecting an arbitrary angle is equivalent to being able to construct a root of a certain cubic equation. It tur ...
History of geometry

Geometry (from the Ancient Greek: γεωμετρία; geo- ""earth"", -metron ""measurement"") arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers (arithmetic).Classic geometry was focused in compass and straightedge constructions. Geometry was revolutionized by Euclid, who introduced mathematical rigor and the axiomatic method still in use today. His book, The Elements is widely considered the most influential textbook of all time, and was known to all educated people in the West until the middle of the 20th century.In modern times, geometric concepts have been generalized to a high level of abstraction and complexity, and have been subjected to the methods of calculus and abstract algebra, so that many modern branches of the field are barely recognizable as the descendants of early geometry. (See Areas of mathematics and Algebraic geometry.)