Download Final Exam Review

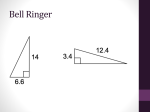
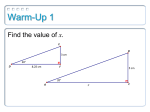
Final Exam Review
Chapter 7 – Right Triangles and
Trigonometry
Geometry
Ms. Rinaldi
Pythagorean Theorem
2
a
+
2
b
=
2
c
Converse of the Pythagorean
Theorem
If…
a2 + b2 = c2 then right
a2 + b2 < c2 then obtuse
a2 + b2 > c2 then acute
45°-45°-90° Triangles
The hypotenuse is
leg.
2 times as long as each
Hypotenuse = leg·
2
30°-60°-90° Triangles
The hypotenuse is twice as long as the shorter leg.
The longer leg is 3 times as long as the shorter leg.
Hypotenuse = 2·shorter leg
Longer leg = shorter leg· 3
Trigonometric Ratios
SOH CAH TOA
opposite
sin 
hypotenuse
adjacent
cos 
hypotenuse
opposite
tan 
adjacent
EXAMPLE
Solve a right triangle
Solve the right triangle. Round decimal answers to
the nearest tenth.
SOLUTION
STEP 1
Find m B by using the Triangle
Sum Theorem.
180o = 90o + 42o + m
48o = m B
B
EXAMPLE
Solve a right triangle (continued)
STEP 2
Approximate BC by using a tangent ratio.
tan 42o = BC
70
70 tan 42o = BC
Write ratio for tangent of 42o.
Multiply each side by 70.
70 0.9004
BC
Approximate tan 42o
63
BC
Simplify and round answer.
EXAMPLE
Solve a right triangle (continued)
STEP 3
Approximate AB by using a cosine ratio.
cos 42o = 70
Write ratio for cosine of 42o.
AB
AB cos 42o =
70
70
AB = cos 42o
70
AB
0.7431
AB
94.2
Multiply each side by AB.
Divide each side by cos 42o.
Use a calculator to find cos 42o.
Simplify .
ANSWER The angle measures are 42o, 48o, and 90o. The
side lengths are 70 feet, about 63 feet, and about 94 feet.