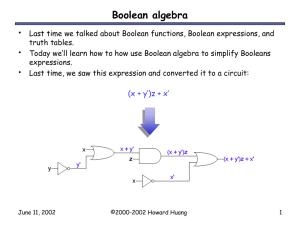
Boolean Algebra
... We can build complex functions from just the basic Boolean values “true” and “false,” and the operations AND, OR and NOT. Any Boolean expression can be implemented with a circuit, which uses primitive logic gates to compute products, sums and complements. We saw two ways to prove equivalence of expr ...
... We can build complex functions from just the basic Boolean values “true” and “false,” and the operations AND, OR and NOT. Any Boolean expression can be implemented with a circuit, which uses primitive logic gates to compute products, sums and complements. We saw two ways to prove equivalence of expr ...
Topological Order and the Kitaev Model
... where n is the electron density. Those states for which this quantity is an integer number are called Integer Quantum Hall states (IQH) whereas those states for which ν is a fractional number are, correspondingly, called Fractional Quantum Hall states (FQH). While the former can be understood from ...
... where n is the electron density. Those states for which this quantity is an integer number are called Integer Quantum Hall states (IQH) whereas those states for which ν is a fractional number are, correspondingly, called Fractional Quantum Hall states (FQH). While the former can be understood from ...
The notion of four-momentum in TGD
... elementary particle spectrum can be understood if Super Virasoro algebra has five tensor factors. Can one decide the fate of the two approaches to EP using this number as an input? 1. For the coset option the situation is unclear. Even the definition of coset representation is problematic. If Super ...
... elementary particle spectrum can be understood if Super Virasoro algebra has five tensor factors. Can one decide the fate of the two approaches to EP using this number as an input? 1. For the coset option the situation is unclear. Even the definition of coset representation is problematic. If Super ...
M04/16
... is an effect algebra. In many cases, these intervals preserve the properties of E. The concepts of local and global sharpness of measurements are introduced. In Section 4 we study measurements with finitely many real values which we call finite measurements. Denoting the set of finite measurements by MF ...
... is an effect algebra. In many cases, these intervals preserve the properties of E. The concepts of local and global sharpness of measurements are introduced. In Section 4 we study measurements with finitely many real values which we call finite measurements. Denoting the set of finite measurements by MF ...
A brief introduction to pre
... Classical and quantum Yang-Baxter equations: Svinolupov and Sokolov(1994), Etingof and Soloviev(1999), Golubschik and Sokolov(2000), · · · Poisson brackets and infinite-dimensional Lie algebras: Gel’fand and Dorfman(1979), Dubrovin and Novikov(1984), Balinskii and Novikov(1985), · · · Quantum field ...
... Classical and quantum Yang-Baxter equations: Svinolupov and Sokolov(1994), Etingof and Soloviev(1999), Golubschik and Sokolov(2000), · · · Poisson brackets and infinite-dimensional Lie algebras: Gel’fand and Dorfman(1979), Dubrovin and Novikov(1984), Balinskii and Novikov(1985), · · · Quantum field ...
Profinite Heyting algebras
... ↓U is clopen for every clopen U ⊆ X Let Upτ (X) denote the Heyting algebra of clopen upsets of X, where U → V = X− ↓(U − V ). Theorem (Esakia 1974). For every Heyting algebra A, there exists an Esakia space (X, ≤) such that A is isomorphic to Upτ (X). ...
... ↓U is clopen for every clopen U ⊆ X Let Upτ (X) denote the Heyting algebra of clopen upsets of X, where U → V = X− ↓(U − V ). Theorem (Esakia 1974). For every Heyting algebra A, there exists an Esakia space (X, ≤) such that A is isomorphic to Upτ (X). ...
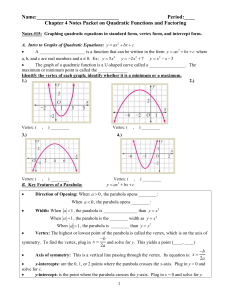
Day 57 - 61 EOC Quadratics Reivew
... Quadratic equations can have two, one, or no solutions (x-intercepts). You can determine how many solutions a quadratic equation has before you solve it by using the ________________. b b2 4ac The discriminant is the expression under the radical in the quadratic formula: x 2a Discriminant ...
... Quadratic equations can have two, one, or no solutions (x-intercepts). You can determine how many solutions a quadratic equation has before you solve it by using the ________________. b b2 4ac The discriminant is the expression under the radical in the quadratic formula: x 2a Discriminant ...
Banach precompact elements of a locally m-convex Bo
... be a semi-topological algebra if A is an algebra with a Hausdorff topology and if the maps: (x, y) 7−→ x + y and (λ, x) 7−→ λx from A × A to A and C×A to A, respectively, are continuous and the map: (x, y) 7−→ xy is separately continuous. A semi - topological algebra is said to be a topological alge ...
... be a semi-topological algebra if A is an algebra with a Hausdorff topology and if the maps: (x, y) 7−→ x + y and (λ, x) 7−→ λx from A × A to A and C×A to A, respectively, are continuous and the map: (x, y) 7−→ xy is separately continuous. A semi - topological algebra is said to be a topological alge ...
Semisimple Varieties of Modal Algebras
... It follows that semisimple varieties have a deduction theorem, that every finitely presentable subdirectly irreducible algebra is splitting. This has useful applications in tense logic. By definition, tense logics are cyclic. K4.2t also is 2–transitive. It follows that its variety is semisimple. A f ...
... It follows that semisimple varieties have a deduction theorem, that every finitely presentable subdirectly irreducible algebra is splitting. This has useful applications in tense logic. By definition, tense logics are cyclic. K4.2t also is 2–transitive. It follows that its variety is semisimple. A f ...
PDF
... C ∗ -algebras are a type of involutive Banach algebras which arise in the study of operators on Hilbert spaces, Lie group representations, locally compact topological spaces, knots, noncommutative geometry, among other topics in mathematics and theoretical physics . Their study was initiated in the ...
... C ∗ -algebras are a type of involutive Banach algebras which arise in the study of operators on Hilbert spaces, Lie group representations, locally compact topological spaces, knots, noncommutative geometry, among other topics in mathematics and theoretical physics . Their study was initiated in the ...
BROCK UNIVERSITY MATHEMATICS MODULES
... to make it easier to work with in some situations. • Why you need it: We complete the square to help us solve a quadratic equation, or to help us determine the vertex of the parabolic graph of a quadratic function. • When to use it: Completing the square will help you determine the vertex of a parab ...
... to make it easier to work with in some situations. • Why you need it: We complete the square to help us solve a quadratic equation, or to help us determine the vertex of the parabolic graph of a quadratic function. • When to use it: Completing the square will help you determine the vertex of a parab ...
In order to integrate general relativity with quantum theory, we
... These simultaneous eigenvalues represent a maximal set of commuting observables for the EP Lie algebra that can be used to index creation and annihilation operators representing particles (fields) with the quantum numbers described. The fundamental entities must be in the representation space of th ...
... These simultaneous eigenvalues represent a maximal set of commuting observables for the EP Lie algebra that can be used to index creation and annihilation operators representing particles (fields) with the quantum numbers described. The fundamental entities must be in the representation space of th ...
Low Dimensional n-Lie Algebras
... theory model for multiple M2-branes (BLG model) based on the metric 3-Lie algebras. More applications of n-Lie algebras in string and membrane theories can be found in [6]-[7]. It is known that up to isomorphisms there is a unique simple finite dimensional n-Lie algebra for n > 2 over an algebraical ...
... theory model for multiple M2-branes (BLG model) based on the metric 3-Lie algebras. More applications of n-Lie algebras in string and membrane theories can be found in [6]-[7]. It is known that up to isomorphisms there is a unique simple finite dimensional n-Lie algebra for n > 2 over an algebraical ...
On congruence extension property for ordered algebras
... B of A is a class of a suitable congruence on A. A variety is called Hamiltonian if all its algebras are Hamiltonian. An unordered algebra is said to have the strong congruence extension property (SCEP) if any congruence θ on a subalgebra B of an algebra A can be extended to a congruence Θ of A in s ...
... B of A is a class of a suitable congruence on A. A variety is called Hamiltonian if all its algebras are Hamiltonian. An unordered algebra is said to have the strong congruence extension property (SCEP) if any congruence θ on a subalgebra B of an algebra A can be extended to a congruence Θ of A in s ...
x+y
... • A field is an example of an algebraic structure – An algebraic structure consists of one or more sets closed under one or more operations, satisfying some axioms. – An axiom is a statement or proposition on which an abstractly defined structure is based. ...
... • A field is an example of an algebraic structure – An algebraic structure consists of one or more sets closed under one or more operations, satisfying some axioms. – An axiom is a statement or proposition on which an abstractly defined structure is based. ...
on h1 of finite dimensional algebras
... The quiver algebra is the vector space of finite linear combinations of paths. The multiplication of two paths is their concatenation if it can be done and 0 otherwise. Each vertex is an idempotent, the sum of all the vertices is the unit element in case Q0 is finite. Some authors are interested in ...
... The quiver algebra is the vector space of finite linear combinations of paths. The multiplication of two paths is their concatenation if it can be done and 0 otherwise. Each vertex is an idempotent, the sum of all the vertices is the unit element in case Q0 is finite. Some authors are interested in ...