Very brief introduction to Conformal Field Theory
... Similar chiral correlators have been considered in the Fractional Quantum Hall effect at filling fraction 5/2. This is the so called Pfaffian state due to Moore and Read. FQHE/CFT correspondence ...
... Similar chiral correlators have been considered in the Fractional Quantum Hall effect at filling fraction 5/2. This is the so called Pfaffian state due to Moore and Read. FQHE/CFT correspondence ...
LECTURES ON SYMPLECTIC REFLECTION ALGEBRAS 2. Algebras of Crawley-Boevey and Holland
... center of CΓ (that is equal to (CΓ)Γ , where the invariants are taken with respect to the adjoint action). For c ∈ (CΓ)Γ we set Hc := C⟨x, y⟩#Γ/(xy − yx − c). This is an algebra introduced by Crawley-Boevey and Holland. They checked that gr Hc = C[x, y]#Γ. We are not going to show this right now, in ...
... center of CΓ (that is equal to (CΓ)Γ , where the invariants are taken with respect to the adjoint action). For c ∈ (CΓ)Γ we set Hc := C⟨x, y⟩#Γ/(xy − yx − c). This is an algebra introduced by Crawley-Boevey and Holland. They checked that gr Hc = C[x, y]#Γ. We are not going to show this right now, in ...
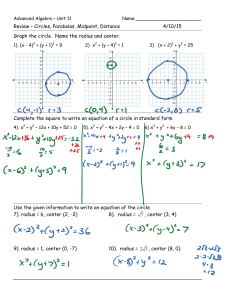
Review – Circles, Parabolas, Midpoint, Distance 4/10/15 Graph the
... Review – Circles, Parabolas, Midpoint, Distance ...
... Review – Circles, Parabolas, Midpoint, Distance ...
Updated 1/26/17 Amanda Havens 530-514-9373 Jr
... Dept. of Math Statistics – Private Tutor – Spring 2017 The tutors on this list are working as independent contractors. They are not hired by the Dept. of Math Statistics at CSU, Chico. Please contact them directly. ...
... Dept. of Math Statistics – Private Tutor – Spring 2017 The tutors on this list are working as independent contractors. They are not hired by the Dept. of Math Statistics at CSU, Chico. Please contact them directly. ...
Symmetry and Integrability of Nonsinglet Sectors in MQM
... MQM non-singlet sector as integrable system Infinite dim symmetry, infinite set of commuting charges Reduction to eigenvalue dynamics (or CalogeroSutherland system) Bosonization : interaction between tachyon and tips Exact eigenstates of the commuting charges: analogy with the matrix string ...
... MQM non-singlet sector as integrable system Infinite dim symmetry, infinite set of commuting charges Reduction to eigenvalue dynamics (or CalogeroSutherland system) Bosonization : interaction between tachyon and tips Exact eigenstates of the commuting charges: analogy with the matrix string ...
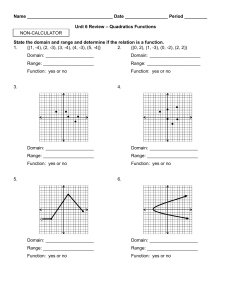
review: quadratics
... Write the equation for the function y = x2 with the following transformations. 20. shift right 4 and up 2 21. reflect across the x-axis, shift left 2 ...
... Write the equation for the function y = x2 with the following transformations. 20. shift right 4 and up 2 21. reflect across the x-axis, shift left 2 ...
Graded decomposition numbers for the
... Theorem 3.3 (Bowman, Cox, S.). Suppose F = C and let λ and µ be one-column l-multipartitions of n. The graded decomposition number [∆(λ) : L(µ)]v is an affine Kazhdan–Lusztig polynomial of affine type Âl−1 . We can compute these efficiently using an algorithm of Soergel’s in an alcove geometry. Not ...
... Theorem 3.3 (Bowman, Cox, S.). Suppose F = C and let λ and µ be one-column l-multipartitions of n. The graded decomposition number [∆(λ) : L(µ)]v is an affine Kazhdan–Lusztig polynomial of affine type Âl−1 . We can compute these efficiently using an algorithm of Soergel’s in an alcove geometry. Not ...
on line
... means the additional structure of a compatible complex-linear involution making the coordinate algebra into a ∗ -algebra. In this case one can denote the above two examples as C[R] and C[S 1 ] when taken with x∗ = x and t ∗ = t −1 respectively. A general Hopf algebra H similarly has the structures ∆ ...
... means the additional structure of a compatible complex-linear involution making the coordinate algebra into a ∗ -algebra. In this case one can denote the above two examples as C[R] and C[S 1 ] when taken with x∗ = x and t ∗ = t −1 respectively. A general Hopf algebra H similarly has the structures ∆ ...
PDF
... We can easily see that kA∗ k = kAk . By the above axioms a C*–algebra is a special case of a Banach algebra where the latter requires the above norm property but not the involution (*) property. Given Banach spaces E, F the space L(E, F ) of (bounded) linear operators from E to F forms a Banach spac ...
... We can easily see that kA∗ k = kAk . By the above axioms a C*–algebra is a special case of a Banach algebra where the latter requires the above norm property but not the involution (*) property. Given Banach spaces E, F the space L(E, F ) of (bounded) linear operators from E to F forms a Banach spac ...
Small Non-Associative Division Algebras up to Isotopy
... see, it can also not have dimension 3. For assume a basis (1, x, y). Since x already has inverse 1 + x, the product xy cannot equal 1. xy = x implies y = 1, a contradiction, and xy = 1 + x means yx = x, also a contradiction. Hence we remain with xy = x + y or yx = x + y. In the first case, (1 + x)(1 ...
... see, it can also not have dimension 3. For assume a basis (1, x, y). Since x already has inverse 1 + x, the product xy cannot equal 1. xy = x implies y = 1, a contradiction, and xy = 1 + x means yx = x, also a contradiction. Hence we remain with xy = x + y or yx = x + y. In the first case, (1 + x)(1 ...
Algebraic Symmetries in Quantum Chemistry
... A “group” is a special collection of “operators” which transform a given set of “vectors” V, among themselves ...
... A “group” is a special collection of “operators” which transform a given set of “vectors” V, among themselves ...
Determinant formulas for the reflection equation algebra
... X p̃1 := q −2i aii is a central element, deforming the trace function on matrices. Note that this is the same expression as for p1 in the FRT algebra, because the twist procedure is identical on linear expressions in the generators. Computer experiments in MAGMA have motivated the following conjectu ...
... X p̃1 := q −2i aii is a central element, deforming the trace function on matrices. Note that this is the same expression as for p1 in the FRT algebra, because the twist procedure is identical on linear expressions in the generators. Computer experiments in MAGMA have motivated the following conjectu ...
Lecture Notes in Physics
... well as for Chap. 10. Chapter 9 deals with an axiomatic approach to two-dimensional conformal field theory. In comparison to the first edition we have added the conformal Ward identities, the state field correspondence, and some changes with respect to the presentation of the operator product expans ...
... well as for Chap. 10. Chapter 9 deals with an axiomatic approach to two-dimensional conformal field theory. In comparison to the first edition we have added the conformal Ward identities, the state field correspondence, and some changes with respect to the presentation of the operator product expans ...
Math 512: The Automorphism Group of the Quaternion Group
... 5). Show that an automorphism of Q is uniquely determined by where it sends i and j. 6.) Let F be a rotational symmetry of the cube. In particular F permutes the faces of the cube (though not completely arbitrarily), and hence their labels ±i, ±j, ±k. Show that F determines an unique automorphism of ...
... 5). Show that an automorphism of Q is uniquely determined by where it sends i and j. 6.) Let F be a rotational symmetry of the cube. In particular F permutes the faces of the cube (though not completely arbitrarily), and hence their labels ±i, ±j, ±k. Show that F determines an unique automorphism of ...
Lecture 8 - Universal Enveloping Algebras and Related Concepts, II
... by π T (l). Further, U (g) is naturally a U (l)-module in the algebra sense. ...
... by π T (l). Further, U (g) is naturally a U (l)-module in the algebra sense. ...
Algebras
... In this chapter we recall very basic facts on general algebra. We state the results without proofs (with the exception of basic properties of derivations) the proof are identical to the similar statement for commutative algebras. ...
... In this chapter we recall very basic facts on general algebra. We state the results without proofs (with the exception of basic properties of derivations) the proof are identical to the similar statement for commutative algebras. ...
1 Towards functional calculus
... identity function f (z) = z to T ? Such a homomorphism of algebras is called a ‘functional calculus’. Recall that an algebra homomorphism is a linear map respecting multiplication, so Ψ(f д) = Ψ(f )Ψ(д), where on the left hand side we mean pointwise multiplication of functions, and on the right hand ...
... identity function f (z) = z to T ? Such a homomorphism of algebras is called a ‘functional calculus’. Recall that an algebra homomorphism is a linear map respecting multiplication, so Ψ(f д) = Ψ(f )Ψ(д), where on the left hand side we mean pointwise multiplication of functions, and on the right hand ...
Titles and Abstracts
... (playing the role of the anticommutator in the case F=2) expresses the zero graded part in terms of the non-zero graded part. This structure enables us to define various non-trivial extensions of the Poincare algebra. These extensions are study more preciselly in two different contexts. The first al ...
... (playing the role of the anticommutator in the case F=2) expresses the zero graded part in terms of the non-zero graded part. This structure enables us to define various non-trivial extensions of the Poincare algebra. These extensions are study more preciselly in two different contexts. The first al ...