A NOTE ON DERIVATIONS OF COMMUTATIVE ALGEBRAS 1199
... is defined in terms of the product xy of A by the rule x o y —xy+yx. By direct calculation, we have (x o y) o z - x o (y o 2) = (x, y, z) + (x, z, y) + (y, x, z) - ...
... is defined in terms of the product xy of A by the rule x o y —xy+yx. By direct calculation, we have (x o y) o z - x o (y o 2) = (x, y, z) + (x, z, y) + (y, x, z) - ...
Chapter 1 Distance Adding Mixed Numbers Fractions of the same
... Multiplication ab = ba (example 3 × 2 = 2 × 3) Addition a + b = b + a (example 3 + 2 = 2 + 3) Subtraction is not commutative 2 − 3 6= 3 − 2 Division is not commutative 2/3 6= 3/2 To use the commutative property write everything in terms of addition and multiplication 6. Think of the work commuter to ...
... Multiplication ab = ba (example 3 × 2 = 2 × 3) Addition a + b = b + a (example 3 + 2 = 2 + 3) Subtraction is not commutative 2 − 3 6= 3 − 2 Division is not commutative 2/3 6= 3/2 To use the commutative property write everything in terms of addition and multiplication 6. Think of the work commuter to ...
PDF
... The category of commutative Hopf algebras is anti-equivalent to the category of affine group schemes. The prime spectrum of a commutative Hopf algebra is an affine group scheme of multiplicative units. And going in the opposite direction, the algebra of natural transformations from an affine group s ...
... The category of commutative Hopf algebras is anti-equivalent to the category of affine group schemes. The prime spectrum of a commutative Hopf algebra is an affine group scheme of multiplicative units. And going in the opposite direction, the algebra of natural transformations from an affine group s ...
LECTURES ON SYMPLECTIC REFLECTION ALGEBRAS Setting. W
... each separate dw acts by 0 on C[h]x . We can represent dw in the form α fα ∂ α , where . . , xn be the dual basis to a1 , . . . , an . We α = (α1 , . . . , αn ) and ∂ α = aα1 1 . . . aαnn . Let x1 , .∑ can prove that fα = 0 by induction on |α| = i αi starting from |α| = 0. For this we consider the a ...
... each separate dw acts by 0 on C[h]x . We can represent dw in the form α fα ∂ α , where . . , xn be the dual basis to a1 , . . . , an . We α = (α1 , . . . , αn ) and ∂ α = aα1 1 . . . aαnn . Let x1 , .∑ can prove that fα = 0 by induction on |α| = i αi starting from |α| = 0. For this we consider the a ...
Algebras. Derivations. Definition of Lie algebra
... variables. 1.1.4. Example If V is a vector space, define an operation by the formula a · b = 0. This is an algebra operation. 1.2. Subalgebras, ideals, quotient algebras. A linear map f : A → B of k-algebras is called homomorphism if f (a · b) = f (a) · f (b) for each a, b ∈ A. The image of a homomo ...
... variables. 1.1.4. Example If V is a vector space, define an operation by the formula a · b = 0. This is an algebra operation. 1.2. Subalgebras, ideals, quotient algebras. A linear map f : A → B of k-algebras is called homomorphism if f (a · b) = f (a) · f (b) for each a, b ∈ A. The image of a homomo ...
Symmetries in Conformal Field Theory
... operation on (0, 1) is multiplication. Indeed any object of A is conformally equivalent to an annulus in the plane, and two such are equivalent if the ratios of the radii of the inner and outer circles coincide. The Diff + (S 1 ) factors describe the parameterisations of the boundary circles. Propos ...
... operation on (0, 1) is multiplication. Indeed any object of A is conformally equivalent to an annulus in the plane, and two such are equivalent if the ratios of the radii of the inner and outer circles coincide. The Diff + (S 1 ) factors describe the parameterisations of the boundary circles. Propos ...
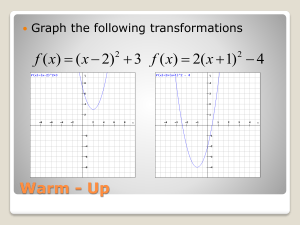
PreCalculus Fall 2014 Lesson 022 _Vertex Equation of a parabola
... Lesson Plan #022 Class: PreCalculus ...
... Lesson Plan #022 Class: PreCalculus ...
PDF
... where each element x ∈ KD(A, λ) has a unique expression x = a + bi. Properties. Let x, y, z will be general elements of KD(A, λ). 1. (xy)∗ = y ∗ x∗ , 2. x + x∗ ∈ A, 3. N (xy) = N (x)N (y). Examples. All examples considered below have ground ring the reals R. • KD(R, −1) = C, the complex numbers. • K ...
... where each element x ∈ KD(A, λ) has a unique expression x = a + bi. Properties. Let x, y, z will be general elements of KD(A, λ). 1. (xy)∗ = y ∗ x∗ , 2. x + x∗ ∈ A, 3. N (xy) = N (x)N (y). Examples. All examples considered below have ground ring the reals R. • KD(R, −1) = C, the complex numbers. • K ...
Open-string operator products
... Thus BRST invariance of W and V requires the background satisfy only the (free) gauge-covariant field equations ∂ b Fba = 0. This was to be expected, since quantum BRST invariance of Yang-Mills in a Yang-Mills background requires the same in field theory. We also find an order α0 correction to the v ...
... Thus BRST invariance of W and V requires the background satisfy only the (free) gauge-covariant field equations ∂ b Fba = 0. This was to be expected, since quantum BRST invariance of Yang-Mills in a Yang-Mills background requires the same in field theory. We also find an order α0 correction to the v ...
Clément Hongler Spring 2016 Lecture Series EPFL
... structures that allow for extremely precise investigations, yielding in particular nonperturbative descriptions with exact formulae. This series will explain how 2D CFT works, in particular how planar lattice models can be understood using the Minimal Models of CFT. While this connection remains lar ...
... structures that allow for extremely precise investigations, yielding in particular nonperturbative descriptions with exact formulae. This series will explain how 2D CFT works, in particular how planar lattice models can be understood using the Minimal Models of CFT. While this connection remains lar ...
Symposium Spring 2015 Schedule
... family of symmetric groups, and in doing so recovered the main results of Young's work (most notably the Young graph) in a more natural way. In this talk, I'll give a broad introduction to Gelfand-Zetlin theory and use it to outline the strategies used in the Okounkov-Vershik approach. ...
... family of symmetric groups, and in doing so recovered the main results of Young's work (most notably the Young graph) in a more natural way. In this talk, I'll give a broad introduction to Gelfand-Zetlin theory and use it to outline the strategies used in the Okounkov-Vershik approach. ...
Universal Enveloping Algebras (and
... object to its more friendly unital associative counterpart U g (allowing for the use of asociative methods such as localization). The reverse is a very natural process: Any associative algebra A over the field k becomes a Lie algebra over k (called the underlying Lie algebra of A, and denoted AL ) w ...
... object to its more friendly unital associative counterpart U g (allowing for the use of asociative methods such as localization). The reverse is a very natural process: Any associative algebra A over the field k becomes a Lie algebra over k (called the underlying Lie algebra of A, and denoted AL ) w ...
PDF
... Let A be an associative algebra over a field K. For a, b ∈ A, the element of A defined by [a, b] = ab − ba is called the commutator of a and b. The corresponding bilinear operation [−, −] : A × A → A is called the commutator bracket. The commutator bracket is bilinear, skew-symmetric, and also satis ...
... Let A be an associative algebra over a field K. For a, b ∈ A, the element of A defined by [a, b] = ab − ba is called the commutator of a and b. The corresponding bilinear operation [−, −] : A × A → A is called the commutator bracket. The commutator bracket is bilinear, skew-symmetric, and also satis ...
LIE-ADMISSIBLE ALGEBRAS AND THE VIRASORO
... HYO CHUL MYUNG∗ ABSTRACT. Third power-associative, Lie-admissible products on the Virasoro algebra are determined in terms of linear functionals and bilinear forms. ...
... HYO CHUL MYUNG∗ ABSTRACT. Third power-associative, Lie-admissible products on the Virasoro algebra are determined in terms of linear functionals and bilinear forms. ...
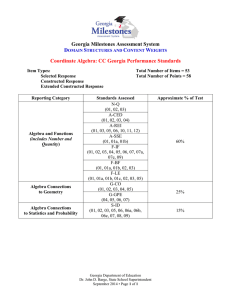
Coordinate Algebra - Georgia Department of Education
... Georgia Milestones Assessment System DOMAIN STRUCTURES AND CONTENT WEIGHTS Coordinate Algebra: CC Georgia Performance Standards Item Types: Selected Response Constructed Response Extended Constructed Response Reporting Category ...
... Georgia Milestones Assessment System DOMAIN STRUCTURES AND CONTENT WEIGHTS Coordinate Algebra: CC Georgia Performance Standards Item Types: Selected Response Constructed Response Extended Constructed Response Reporting Category ...
Quadratic Functions Extreme Values and Graphs
... Vertex Extreme Value Standard Form Vertex Form ...
... Vertex Extreme Value Standard Form Vertex Form ...
PDF
... Moreover, consider the classical configuration space Q = R3 of a classical, mechanical system, or particle whose phase space is the cotangent bundle T ∗ R3 ∼ = R6 , for which the space of (classical) observables is taken to be the real vector space of smooth functions on M , and with T being an elem ...
... Moreover, consider the classical configuration space Q = R3 of a classical, mechanical system, or particle whose phase space is the cotangent bundle T ∗ R3 ∼ = R6 , for which the space of (classical) observables is taken to be the real vector space of smooth functions on M , and with T being an elem ...