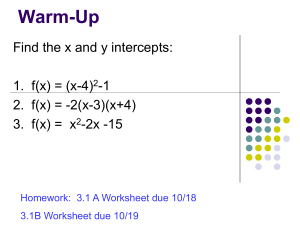
Warm-Up
... a. Determine, without graphing, whether the function has a minimum value or a maximum value. b. Find the max. or min. value and determine where it occurs c. Identify the function’s domain and range. ...
... a. Determine, without graphing, whether the function has a minimum value or a maximum value. b. Find the max. or min. value and determine where it occurs c. Identify the function’s domain and range. ...
PDF
... the distributive axiom we cannot establish connections between addition and multiplication. Without scalar multiplication we cannot describe coefficients. With these equations we can define certain subalgebras, for example we see both axioms at work in Proposition 2. Given an algebra A, the set Z0 ( ...
... the distributive axiom we cannot establish connections between addition and multiplication. Without scalar multiplication we cannot describe coefficients. With these equations we can define certain subalgebras, for example we see both axioms at work in Proposition 2. Given an algebra A, the set Z0 ( ...
please click here
... Unique Number: 56055 Meeting Time: Monday–Wednesday–Friday, 10:00 am to 11:00 am Room: RLM 9.166 Text: Abstract Algebra, 3rd edition by Dummit and Foote, published by Wiley Brief Course Description: This course is a continuation of the fall graduate algebra course M380C, currently taught by David He ...
... Unique Number: 56055 Meeting Time: Monday–Wednesday–Friday, 10:00 am to 11:00 am Room: RLM 9.166 Text: Abstract Algebra, 3rd edition by Dummit and Foote, published by Wiley Brief Course Description: This course is a continuation of the fall graduate algebra course M380C, currently taught by David He ...
PDF
... ∗ hAlgebraFormedFromACategoryi created: h2013-03-21i by: hrspuzioi version: h38686i Privacy setting: h1i hDefinitioni h18A05i † This text is available under the Creative Commons Attribution/Share-Alike License 3.0. You can reuse this document or portions thereof only if you do so under terms that ar ...
... ∗ hAlgebraFormedFromACategoryi created: h2013-03-21i by: hrspuzioi version: h38686i Privacy setting: h1i hDefinitioni h18A05i † This text is available under the Creative Commons Attribution/Share-Alike License 3.0. You can reuse this document or portions thereof only if you do so under terms that ar ...