Classical and intuitionistic relation algebras
... as functional elements if and only if it is the complex algebra of a generalized Brandt groupoid. The results about canonical extensions were extended to distributive lattices with operators by Gehrke and Jónsson in 1994, and to lattices with operators by Gehrke and Harding in 2001. Here we show re ...
... as functional elements if and only if it is the complex algebra of a generalized Brandt groupoid. The results about canonical extensions were extended to distributive lattices with operators by Gehrke and Jónsson in 1994, and to lattices with operators by Gehrke and Harding in 2001. Here we show re ...
Division Algebras
... In addition to the “external” Cayley-Dickson construction for a unital composition algebra, there is also an “internal” version: Proposition. Given a unital composition algebra A and a finite-dimensional composition subalgebra A0 ⊂ A with A0 = 6 A, there is a subalgebra B 0 ⊂ A such that A0 ⊕ B 0 ⊂ ...
... In addition to the “external” Cayley-Dickson construction for a unital composition algebra, there is also an “internal” version: Proposition. Given a unital composition algebra A and a finite-dimensional composition subalgebra A0 ⊂ A with A0 = 6 A, there is a subalgebra B 0 ⊂ A such that A0 ⊕ B 0 ⊂ ...
BABY VERMA MODULES FOR RATIONAL CHEREDNIK ALGEBRAS
... for x, x ∈ h and y, y ∈ h. Note that this definition does not depend on the choice of αs and αs∨ . This algebra is naturally Z-graded, setting deg W = 0, deg h∗ = 1, and deg h = −1. One may also view the parameters t, c as formal variables to obtain a universal Cherednik algebra H, of which Ht,c is ...
... for x, x ∈ h and y, y ∈ h. Note that this definition does not depend on the choice of αs and αs∨ . This algebra is naturally Z-graded, setting deg W = 0, deg h∗ = 1, and deg h = −1. One may also view the parameters t, c as formal variables to obtain a universal Cherednik algebra H, of which Ht,c is ...
Section 3.3B Word Problems
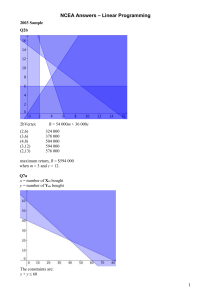
... Answer: $950 per month for rent max revenue = $54,150 Let x = number of $50 increases Let R = revenue ...
... Answer: $950 per month for rent max revenue = $54,150 Let x = number of $50 increases Let R = revenue ...
Lie Algebras and the Schr¨odinger equation: (quasi-exact-solvability, symmetric coordinates) Alexander Turbiner
... where P2 is a polynomial of second degree in the generators J of the maximal affine subalgebra of the algebra glN+1 in realization (∗). Hence glN+1 is their hidden algebra. From this viewpoint all four models are different faces of a single ...
... where P2 is a polynomial of second degree in the generators J of the maximal affine subalgebra of the algebra glN+1 in realization (∗). Hence glN+1 is their hidden algebra. From this viewpoint all four models are different faces of a single ...
An Integration of General Relativity and Relativistic Quantum
... Einstein equations cannot come from the RQT but rather from the SM operators acting on the state of the current system. (In practice, it comes from large masses such as black holes or stars and thus the classical expression is valid). ...
... Einstein equations cannot come from the RQT but rather from the SM operators acting on the state of the current system. (In practice, it comes from large masses such as black holes or stars and thus the classical expression is valid). ...
Universal enveloping algebra
... 17. Universal enveloping algebras Recall that, for an associative algebra A with unity (1), a Lie algebra structure on A is given by the Lie bracket [ab] = ab − ba. Let L(A) denote this Lie algebra. Then L is a functor which converts associative algebras into Lie algebras. Every Lie algebra L has a ...
... 17. Universal enveloping algebras Recall that, for an associative algebra A with unity (1), a Lie algebra structure on A is given by the Lie bracket [ab] = ab − ba. Let L(A) denote this Lie algebra. Then L is a functor which converts associative algebras into Lie algebras. Every Lie algebra L has a ...
PDF
... • Alternatively, a normed algebra A can be defined as a normed vector space with a multiplication defined on A such that multiplication is continuous with respect to the norm k · k. • Typically, k is either the reals R or the complex numbers C, and A is called a real normed algebra or a complex norm ...
... • Alternatively, a normed algebra A can be defined as a normed vector space with a multiplication defined on A such that multiplication is continuous with respect to the norm k · k. • Typically, k is either the reals R or the complex numbers C, and A is called a real normed algebra or a complex norm ...
HURWITZ` THEOREM 1. Introduction In this article we describe
... In this article we describe several results based on the paper [Hur98] and which we will refer to as Hurwitz’ theorem. There are several related results: the classification of real normed division algebras, the classification of complex composition algebras and the classification of real composition ...
... In this article we describe several results based on the paper [Hur98] and which we will refer to as Hurwitz’ theorem. There are several related results: the classification of real normed division algebras, the classification of complex composition algebras and the classification of real composition ...
slides
... Change of basis - step 2 of 2 • define new basis for expressing parabose anticommutators: ...
... Change of basis - step 2 of 2 • define new basis for expressing parabose anticommutators: ...
Solutions
... 5) An integer is called snakelike if its decimal representation a1a2 a3 ak satisfies ai ai 1 if i is odd, and ai ai 1 if i is even. How many snakelike integers between 1000 and 9999 have 4 distinct digits. Solution: Let us suppose a four digit number is snakelike. Then it is of the form a b ...
... 5) An integer is called snakelike if its decimal representation a1a2 a3 ak satisfies ai ai 1 if i is odd, and ai ai 1 if i is even. How many snakelike integers between 1000 and 9999 have 4 distinct digits. Solution: Let us suppose a four digit number is snakelike. Then it is of the form a b ...
Lie Algebras - Fakultät für Mathematik
... whereas the coefficient of x ⊗ u[0] + u[0] ⊗ x at u[0] ⊗ u[0] is 2x1 . Since the elements in C(1) are primitive, we may assume that d(M1 ) ≥ 2. Take a direct decomposition [M1′ ⊕ M1′′ ] = [M1 ], with an indecomposable object M1′ , then x1 is the coefficient at u[M1′ ] ⊗ u[M1′′ ] for ∆(x). On the oth ...
... whereas the coefficient of x ⊗ u[0] + u[0] ⊗ x at u[0] ⊗ u[0] is 2x1 . Since the elements in C(1) are primitive, we may assume that d(M1 ) ≥ 2. Take a direct decomposition [M1′ ⊕ M1′′ ] = [M1 ], with an indecomposable object M1′ , then x1 is the coefficient at u[M1′ ] ⊗ u[M1′′ ] for ∆(x). On the oth ...
COCOMMUTATIVE HOPF ALGEBRAS WITH ANTIPODE We shall
... For p>0, we generalize the Birkhoff-Witt theorem by introducing the notion of divided powers. These also play a role in the theory of algebraic groups where certain sequences of divided powers correspond to one parameter subgroups. The divided powers appear in a "Galois Theory" for all finite normal ...
... For p>0, we generalize the Birkhoff-Witt theorem by introducing the notion of divided powers. These also play a role in the theory of algebraic groups where certain sequences of divided powers correspond to one parameter subgroups. The divided powers appear in a "Galois Theory" for all finite normal ...
(8 pp Preprint)
... Example/Remark (ordinary Lie derivatives) A good way to understand the principle at work here is to compare this to the infinitesimal version, which may be more familiar. Consider the 2-category whose objects are differential graded commutative algebras, whose morphisms are linear maps that are both ...
... Example/Remark (ordinary Lie derivatives) A good way to understand the principle at work here is to compare this to the infinitesimal version, which may be more familiar. Consider the 2-category whose objects are differential graded commutative algebras, whose morphisms are linear maps that are both ...