Ch 6
... headwind. At the same time, Plane B flies form Los Angeles to Charlotte at a rate of 550 mi/h with a tailwind. The air speed of each plane is the same. The ground speeds are shown below. What is the air speed? What is the wind speed? ...
... headwind. At the same time, Plane B flies form Los Angeles to Charlotte at a rate of 550 mi/h with a tailwind. The air speed of each plane is the same. The ground speeds are shown below. What is the air speed? What is the wind speed? ...
http://redshift.vif.com/JournalFiles/V13NO2PDF/V13N2DMI.pdf
... bubble in a turbulent fluid models the neutron. The selfenergy of a bubble is defined as the work performed against the pressure of the fluid in order to create the bubble. The mass of the neutron corresponds to the mass of the equilibrium vapor in the bubble. Taking the vapor to be an ideal gas the ...
... bubble in a turbulent fluid models the neutron. The selfenergy of a bubble is defined as the work performed against the pressure of the fluid in order to create the bubble. The mass of the neutron corresponds to the mass of the equilibrium vapor in the bubble. Taking the vapor to be an ideal gas the ...
Lecture 27
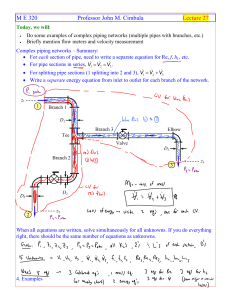
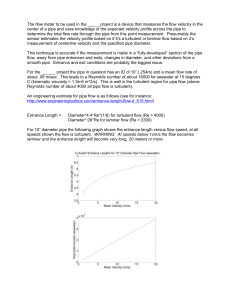
... Background: In some applications (e.g., nuclear reactor cooling), it is critical that the volume flow rate of a fluid remains constant, regardless of head changes in the system downstream (within specified limits, of course). One method of ensuring a constant volume flow rate is to install an oversi ...
... Background: In some applications (e.g., nuclear reactor cooling), it is critical that the volume flow rate of a fluid remains constant, regardless of head changes in the system downstream (within specified limits, of course). One method of ensuring a constant volume flow rate is to install an oversi ...
COURSE CONTENT MATHEMATICAL ECONOMICS
... functions subject to linear constraints. Duality in linear programming: the primal and the dual LP problem, sensitivity analysis. Methods of solution: the graphical method, the Simplex method. Applications in economics. (C) Dynamic Programming. Introduction to differential equations, differential eq ...
... functions subject to linear constraints. Duality in linear programming: the primal and the dual LP problem, sensitivity analysis. Methods of solution: the graphical method, the Simplex method. Applications in economics. (C) Dynamic Programming. Introduction to differential equations, differential eq ...
The Bernoulli equation
... ie Potential Energy + Kinetic Energy + Pressure Energy = Total Energy H Equations (1) and (2) are special cases of Bernoulli's equation. If p1 = p2, equation (2) applies. If v1 =v2 (zero velocity difference) equation (1) applies. Bernoulli's equation has some restrictions in its applicability, they ...
... ie Potential Energy + Kinetic Energy + Pressure Energy = Total Energy H Equations (1) and (2) are special cases of Bernoulli's equation. If p1 = p2, equation (2) applies. If v1 =v2 (zero velocity difference) equation (1) applies. Bernoulli's equation has some restrictions in its applicability, they ...
Homogeneous Equations with Constant Coefficients
... MAT 285 Spring Semester 2012-13 Lecture 15 Notes These notes correspond to Section 3.1 in the text. ...
... MAT 285 Spring Semester 2012-13 Lecture 15 Notes These notes correspond to Section 3.1 in the text. ...
Coriolis effect - public.asu.edu
... The momentum equation in the rotating coordinate system has two extra terms: Term (A): Coriolis force Term (B): Centrifugal force They are "fictitious forces" that arises from the coordinate transformation. They are perpendicular to the velocity vector so can only act to change the "direction" of mo ...
... The momentum equation in the rotating coordinate system has two extra terms: Term (A): Coriolis force Term (B): Centrifugal force They are "fictitious forces" that arises from the coordinate transformation. They are perpendicular to the velocity vector so can only act to change the "direction" of mo ...
Practice Exam
... b) For each of the critical points (equilibria) in a), determine whether they are stable, asymptotically stable, or unstable. 7. (Final Fall 1998 Problem 6) For the linear system of differential equations x1 x1 3x2 , x2 3x1 x2 . a) Write the system in matrix-vector form x Ax . b) Find ...
... b) For each of the critical points (equilibria) in a), determine whether they are stable, asymptotically stable, or unstable. 7. (Final Fall 1998 Problem 6) For the linear system of differential equations x1 x1 3x2 , x2 3x1 x2 . a) Write the system in matrix-vector form x Ax . b) Find ...
Worksheet
... 2) For the conic 2 x 2 − 3 xy + 3 y 2 − 4 x − 2 y − 5 = 0 , answer the following: a) Use the discriminant to determine the type of conic. b) Determine the angle of rotation for the axes. c) Use your calculator to generate a table of values and graph the conic on graph paper. 3) At t = 0, two particl ...
... 2) For the conic 2 x 2 − 3 xy + 3 y 2 − 4 x − 2 y − 5 = 0 , answer the following: a) Use the discriminant to determine the type of conic. b) Determine the angle of rotation for the axes. c) Use your calculator to generate a table of values and graph the conic on graph paper. 3) At t = 0, two particl ...
Trig_Equations
... AS90292 Mathematics 2.9 Solve straightforward trigonometric equations Level 2 ...
... AS90292 Mathematics 2.9 Solve straightforward trigonometric equations Level 2 ...
"Is affirmed"
... questions and decisions receptions and to clear up them by the medium of teacher. Final knowledge and skills: Students should know: 1. Governed finding derivative of basic functions. 2. Governed finding of derivative sum, work, particle and complicated function. Students should be able: 1. To find s ...
... questions and decisions receptions and to clear up them by the medium of teacher. Final knowledge and skills: Students should know: 1. Governed finding derivative of basic functions. 2. Governed finding of derivative sum, work, particle and complicated function. Students should be able: 1. To find s ...
Computational fluid dynamics

Computational fluid dynamics, usually abbreviated as CFD, is a branch of fluid mechanics that uses numerical analysis and algorithms to solve and analyze problems that involve fluid flows. Computers are used to perform the calculations required to simulate the interaction of liquids and gases with surfaces defined by boundary conditions. With high-speed supercomputers, better solutions can be achieved. Ongoing research yields software that improves the accuracy and speed of complex simulation scenarios such as transonic or turbulent flows. Initial experimental validation of such software is performed using a wind tunnel with the final validation coming in full-scale testing, e.g. flight tests.