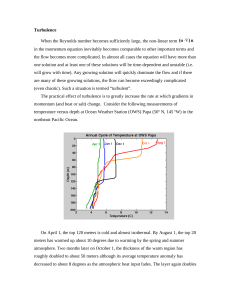
Turbulence When the Reynolds number becomes sufficiently large
... the flow becomes more complicated. In almost all cases the equation will have more than one solution and at least one of these solutions will be time-dependent and unstable (i.e. will grow with time). Any growing solution will quickly dominate the flow and if there are many of these growing solution ...
... the flow becomes more complicated. In almost all cases the equation will have more than one solution and at least one of these solutions will be time-dependent and unstable (i.e. will grow with time). Any growing solution will quickly dominate the flow and if there are many of these growing solution ...
Transport Equations: An Attempt of Analytical Solution and Application
... CE291 Term Project Di Jin Zeshi Zheng ...
... CE291 Term Project Di Jin Zeshi Zheng ...
Mathematical model EXCEL SHEET
... Stimulus - response technique (injection of a tracer and measurement responses) has proved to be useful for detection of cross-flow. As tracers KCl (conductivity method), KMnO4 (visualisation), Tc99 (radioisotope) were used. Conductivity method is superior at isothermal flows, while radioisotopes ar ...
... Stimulus - response technique (injection of a tracer and measurement responses) has proved to be useful for detection of cross-flow. As tracers KCl (conductivity method), KMnO4 (visualisation), Tc99 (radioisotope) were used. Conductivity method is superior at isothermal flows, while radioisotopes ar ...
CEE161A/264A: Rivers, Streams, and Canals Summer Quarter 2012
... Rivers, Streams, and Canals is a class dedicated to understanding a branch of fluid dynamics often referred to as Open Channel Flow/Hydraulics, i.e., the flow in channels with a free surface that is ...
... Rivers, Streams, and Canals is a class dedicated to understanding a branch of fluid dynamics often referred to as Open Channel Flow/Hydraulics, i.e., the flow in channels with a free surface that is ...
The flow of a vector field. Suppose F = Pi + Qj is a vector field in the
... That is, for each (x, y), t 7→ ft (x, y) is a path whose velocity at time t is the vector that F assigns to ft (x, y). Example. Let F = −yi + xj. Draw a picture of F. Note that ft (x, y) = (x cos t − y sin t, x sin t + y cos t). That is, ft is counterclockwise rotation of R2 through an angle of t ra ...
... That is, for each (x, y), t 7→ ft (x, y) is a path whose velocity at time t is the vector that F assigns to ft (x, y). Example. Let F = −yi + xj. Draw a picture of F. Note that ft (x, y) = (x cos t − y sin t, x sin t + y cos t). That is, ft is counterclockwise rotation of R2 through an angle of t ra ...
Using Dimensions
... Some of the most interesting results of hydrodynamics, such as the sixteen-fold increase in flow down a pipe on doubling the radius, can actually be found without doing any calculations, just from dimensional considerations. We symbolize the “dimensions” mass, length and time by M, L, T. We then wri ...
... Some of the most interesting results of hydrodynamics, such as the sixteen-fold increase in flow down a pipe on doubling the radius, can actually be found without doing any calculations, just from dimensional considerations. We symbolize the “dimensions” mass, length and time by M, L, T. We then wri ...
Notes #11
... is no external applied force acting on the chosen control volume, then f must be zero. This can readily be verified by direct analytical computations. What happens if one choses a control volume which includes a singular point? First of all, by the logic of the previous paragraph, we know that any c ...
... is no external applied force acting on the chosen control volume, then f must be zero. This can readily be verified by direct analytical computations. What happens if one choses a control volume which includes a singular point? First of all, by the logic of the previous paragraph, we know that any c ...
Numerical Solution of Hyperbolic Telegraph Equation Using Method
... In this work, to minimize the residual function along the whole domain the collocation method and partition method were used. For the collocation method the residual is then collocated at equally space point and equated to zero while for the partition method, the domain is subdivided into subdomain ...
... In this work, to minimize the residual function along the whole domain the collocation method and partition method were used. For the collocation method the residual is then collocated at equally space point and equated to zero while for the partition method, the domain is subdivided into subdomain ...
1.3 Solving Equations
... You can multiply the same number, except zero, to both side of an equation. ...
... You can multiply the same number, except zero, to both side of an equation. ...
00410021.pdf
... considered and the values for interface cell values are obtained through interpolations. The steady incompressible 3D Reynolds-Averaged Navier-Stokes (RANS) equations are solved using a second-order implicit, cell-centered, finite volume scheme on Cartesian non-uniform grids. SIMPLE (Semi-Implicit M ...
... considered and the values for interface cell values are obtained through interpolations. The steady incompressible 3D Reynolds-Averaged Navier-Stokes (RANS) equations are solved using a second-order implicit, cell-centered, finite volume scheme on Cartesian non-uniform grids. SIMPLE (Semi-Implicit M ...
1 Surface Integrals Mass problem. Find the mass M of a curved
... Net volume is the volume that passes through σ in the positive direction minus the volume that passes through σ in the negative direction. Velocity of the fluid F~ (x, y, z) = f (x, y, z)~i + g(x, y, z) ~j + h(x, y, z) ~k ~n is the unit normal toward the positive side of σ. (F~ · ~n) ~n is the proje ...
... Net volume is the volume that passes through σ in the positive direction minus the volume that passes through σ in the negative direction. Velocity of the fluid F~ (x, y, z) = f (x, y, z)~i + g(x, y, z) ~j + h(x, y, z) ~k ~n is the unit normal toward the positive side of σ. (F~ · ~n) ~n is the proje ...
Computational fluid dynamics

Computational fluid dynamics, usually abbreviated as CFD, is a branch of fluid mechanics that uses numerical analysis and algorithms to solve and analyze problems that involve fluid flows. Computers are used to perform the calculations required to simulate the interaction of liquids and gases with surfaces defined by boundary conditions. With high-speed supercomputers, better solutions can be achieved. Ongoing research yields software that improves the accuracy and speed of complex simulation scenarios such as transonic or turbulent flows. Initial experimental validation of such software is performed using a wind tunnel with the final validation coming in full-scale testing, e.g. flight tests.























