Handout16B
... Now, those of you with some biochemistry experience might argue that to analyze the molecules that comprise a cell, it is rather difficult to extract them without breakage. Thus, if you find a strand of RNA, you may not be seeing the whole strand from start to finish and so the segment that you are ...
... Now, those of you with some biochemistry experience might argue that to analyze the molecules that comprise a cell, it is rather difficult to extract them without breakage. Thus, if you find a strand of RNA, you may not be seeing the whole strand from start to finish and so the segment that you are ...
Lecture 15: Projections onto subspaces
... Figure 1: The point closest to b on the line determined by a. We can see from Figure 1 that this closest point p is at the intersection formed by a line through b that is orthogonal to a. If we think of p as an approximation of b, then the length of e = b − p is the error in that approxi mation. We ...
... Figure 1: The point closest to b on the line determined by a. We can see from Figure 1 that this closest point p is at the intersection formed by a line through b that is orthogonal to a. If we think of p as an approximation of b, then the length of e = b − p is the error in that approxi mation. We ...
Ch 16 Geometric Transformations and Vectors Combined Version 2
... Note: 2 vectors w/same magnitude & direction are considered to be equivalent vectors, no matter their locations ...
... Note: 2 vectors w/same magnitude & direction are considered to be equivalent vectors, no matter their locations ...
3.8
... Third, the nucleotide at the site is C at time t but will change to A at t 1 , a transversional change. The probabilities for the two events are pC (t ) and , respectively, and their product constitutes the third term in Equation. Fourth, the nucleotide at the site is G at time t but will change ...
... Third, the nucleotide at the site is C at time t but will change to A at t 1 , a transversional change. The probabilities for the two events are pC (t ) and , respectively, and their product constitutes the third term in Equation. Fourth, the nucleotide at the site is G at time t but will change ...
DIAGONALIZATION OF MATRICES OF CONTINUOUS FUNCTIONS
... X is completely determined by its first Chern class c1 (L) ∈ H 2 (X, Z). But π1 (X) and π2 (X) are both trivial by hypothesis, so H 2 (X, Z) = 0 by Hurewicz’s theorem. Thus we can pick a continuous non-vanishing section fi of ran Qi for each i. By applying the Gram-Schmidt procedure (which is contin ...
... X is completely determined by its first Chern class c1 (L) ∈ H 2 (X, Z). But π1 (X) and π2 (X) are both trivial by hypothesis, so H 2 (X, Z) = 0 by Hurewicz’s theorem. Thus we can pick a continuous non-vanishing section fi of ran Qi for each i. By applying the Gram-Schmidt procedure (which is contin ...
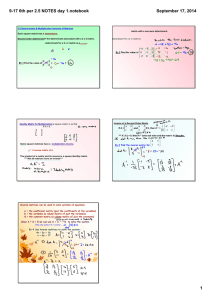
917 6th per 2.5 NOTES day 1.notebook September 17, 2014
... 917 6th per 2.5 NOTES day 1.notebook ...
... 917 6th per 2.5 NOTES day 1.notebook ...
PDF
... Let R be a commutative ring with 1 6= 0. An R-algebra A with multiplication not assumed to be associative is called a (commutative) Jordan algebra if 1. A is commutative: ab = ba, and 2. A satisfies the Jordan identity: (a2 b)a = a2 (ba), for any a, b ∈ A. The above can be restated as 1. [A, A] = 0, ...
... Let R be a commutative ring with 1 6= 0. An R-algebra A with multiplication not assumed to be associative is called a (commutative) Jordan algebra if 1. A is commutative: ab = ba, and 2. A satisfies the Jordan identity: (a2 b)a = a2 (ba), for any a, b ∈ A. The above can be restated as 1. [A, A] = 0, ...
Jordan normal form
In linear algebra, a Jordan normal form (often called Jordan canonical form)of a linear operator on a finite-dimensional vector space is an upper triangular matrix of a particular form called a Jordan matrix, representing the operator with respect to some basis. Such matrix has each non-zero off-diagonal entry equal to 1, immediately above the main diagonal (on the superdiagonal), and with identical diagonal entries to the left and below them. If the vector space is over a field K, then a basis with respect to which the matrix has the required form exists if and only if all eigenvalues of the matrix lie in K, or equivalently if the characteristic polynomial of the operator splits into linear factors over K. This condition is always satisfied if K is the field of complex numbers. The diagonal entries of the normal form are the eigenvalues of the operator, with the number of times each one occurs being given by its algebraic multiplicity.If the operator is originally given by a square matrix M, then its Jordan normal form is also called the Jordan normal form of M. Any square matrix has a Jordan normal form if the field of coefficients is extended to one containing all the eigenvalues of the matrix. In spite of its name, the normal form for a given M is not entirely unique, as it is a block diagonal matrix formed of Jordan blocks, the order of which is not fixed; it is conventional to group blocks for the same eigenvalue together, but no ordering is imposed among the eigenvalues, nor among the blocks for a given eigenvalue, although the latter could for instance be ordered by weakly decreasing size.The Jordan–Chevalley decomposition is particularly simple with respect to a basis for which the operator takes its Jordan normal form. The diagonal form for diagonalizable matrices, for instance normal matrices, is a special case of the Jordan normal form.The Jordan normal form is named after Camille Jordan.