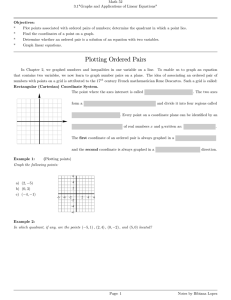
Math 142–Rodriguez Lehmann–3.1 system of linear equations
... I. Systems of Linear Equations A. A system of linear equations in two variables consists of two (or more) equations of the form Ax + By = C, where A, B and C are real numbers. ...
... I. Systems of Linear Equations A. A system of linear equations in two variables consists of two (or more) equations of the form Ax + By = C, where A, B and C are real numbers. ...
File
... 7.EE.4a. Solve word problems leading to equations of the form px + q = r and p(x + q) = r, where p, q, and r are specific rational numbers. Solve equations of these forms fluently. Compare an algebraic solution to an arithmetic solution, identifying the sequence of the operations used in each approa ...
... 7.EE.4a. Solve word problems leading to equations of the form px + q = r and p(x + q) = r, where p, q, and r are specific rational numbers. Solve equations of these forms fluently. Compare an algebraic solution to an arithmetic solution, identifying the sequence of the operations used in each approa ...
Name
... Use substitution to solve each system of equations. If the system does not have exactly one solution, state whether it has no solution or infinitely many solutions. ...
... Use substitution to solve each system of equations. If the system does not have exactly one solution, state whether it has no solution or infinitely many solutions. ...
[ ) Trigonometric Equations — 7.2 π
... Sine, cosine, cosecant and secant all have a period of 2π . Tangent and cotangent have a period of π If the equation has more than one trigonometric function (or a single trigonometric function raised to a power), try getting a zero on one side and factoring. Remember that you may use identities to ...
... Sine, cosine, cosecant and secant all have a period of 2π . Tangent and cotangent have a period of π If the equation has more than one trigonometric function (or a single trigonometric function raised to a power), try getting a zero on one side and factoring. Remember that you may use identities to ...
June - Uniservity CLC
... You must ensure that your answers to parts of questions are clearly labelled. You must show sufficient working to make your methods clear to the Examiner. Answers without working may not gain full credit. ...
... You must ensure that your answers to parts of questions are clearly labelled. You must show sufficient working to make your methods clear to the Examiner. Answers without working may not gain full credit. ...
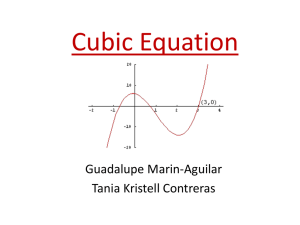
Cubic Equation - Cloudfront.net
... this formula can be used to find the critical points of a cubic function. It turns out that, if , then the cubic function will have two critical points — a local maximum and a local minimum; if , then there is one critical point, and it will yield the inflection point; if , then there are no critica ...
... this formula can be used to find the critical points of a cubic function. It turns out that, if , then the cubic function will have two critical points — a local maximum and a local minimum; if , then there is one critical point, and it will yield the inflection point; if , then there are no critica ...
solving the system
... Each line has infinitely many pairs (x, y) that satisfy it. But taken together, only one pair (3, -2) satisfies both. Finding this pair is called solving the system. In 3.1, you learned to solve a system of two equations in two variables by graphing (approximation). In this section you will learn tw ...
... Each line has infinitely many pairs (x, y) that satisfy it. But taken together, only one pair (3, -2) satisfies both. Finding this pair is called solving the system. In 3.1, you learned to solve a system of two equations in two variables by graphing (approximation). In this section you will learn tw ...
Partial differential equation

In mathematics, a partial differential equation (PDE) is a differential equation that contains unknown multivariable functions and their partial derivatives. (A special case are ordinary differential equations (ODEs), which deal with functions of a single variable and their derivatives.) PDEs are used to formulate problems involving functions of several variables, and are either solved by hand, or used to create a relevant computer model.PDEs can be used to describe a wide variety of phenomena such as sound, heat, electrostatics, electrodynamics, fluid flow, elasticity, or quantum mechanics. These seemingly distinct physical phenomena can be formalised similarly in terms of PDEs. Just as ordinary differential equations often model one-dimensional dynamical systems, partial differential equations often model multidimensional systems. PDEs find their generalisation in stochastic partial differential equations.