* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download [ ) Trigonometric Equations — 7.2 π
Path integral formulation wikipedia , lookup
Two-body problem in general relativity wikipedia , lookup
Two-body Dirac equations wikipedia , lookup
Debye–Hückel equation wikipedia , lookup
BKL singularity wikipedia , lookup
Schrödinger equation wikipedia , lookup
Navier–Stokes equations wikipedia , lookup
Euler equations (fluid dynamics) wikipedia , lookup
Dirac equation wikipedia , lookup
Equations of motion wikipedia , lookup
Van der Waals equation wikipedia , lookup
Derivation of the Navier–Stokes equations wikipedia , lookup
Itô diffusion wikipedia , lookup
Differential equation wikipedia , lookup
Schwarzschild geodesics wikipedia , lookup
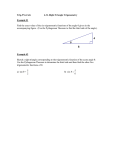
Math 4 Pre-Calculus Name________________________ Date_________________________ Trigonometric Equations — 7.2 Tips for Solving Trigonometric Equations 1. Use the unit circle to find angles between [ 0 , 2π ) that satisfy the equation. 2. 3. 4. 5. 6. Sine, cosine, cosecant and secant all have a period of 2π . Tangent and cotangent have a period of π If the equation has more than one trigonometric function (or a single trigonometric function raised to a power), try getting a zero on one side and factoring. Remember that you may use identities to get an equation in terms of only one trigonometric function. The arguments of the trigonometric functions usually need to be consistent (the same). This will come up in 7.3 & 7.4. Find all solutions of the equation. 1 2 1. sin x = − 2. cs cθ s i n θ = 1 3. cos 4. π 3 − t a n2 x − = 0 2 5. ( s i n t − 1) c o s t 6. s e cθ cs cθ = 2 c scθ 7. 3 sin t + cos t = 1 8. 1 2 x=− 4 2 =0 2sin t csct − csc t = 4sin t − 2 Approximate, to the nearest 1 0′ , the solutions of the equation in the interval [ 0 ° , 3 6 0 ° ) . 9. c o s2 t − 4 c o s t + 2 = 0