Trigonometry Worksheet 1. Pythagorean Theorem refresher If a right
... 1.2 (ii) The figure below shows a point with coordinates (−x, y) on the unit circle and in the second quadrant. Draw a right triangle with the line segment from the origin to the point as its hypotenuse and label the lengths of the sides. [figure here] 1.2 (iii) and (iv) Draw appropriate figures in ...
... 1.2 (ii) The figure below shows a point with coordinates (−x, y) on the unit circle and in the second quadrant. Draw a right triangle with the line segment from the origin to the point as its hypotenuse and label the lengths of the sides. [figure here] 1.2 (iii) and (iv) Draw appropriate figures in ...
Precalculus Final Exam Review
... 7. Let d be the miles driven in the rental car, and let c be the cost in dollars of renting the car. Which of the following formulas is correct?. (a) 4d = :054c ...
... 7. Let d be the miles driven in the rental car, and let c be the cost in dollars of renting the car. Which of the following formulas is correct?. (a) 4d = :054c ...
Lesson 4
... I want to talk about the basis of trigonometry, the unit circle. Draw a coordinate plane and only mark one unit in each direction.. Draw a circle that is centered at the origin and has a radius of one. This is the unit circle. Mark you x-axis and y-axis and also write cosine next to the x and sine n ...
... I want to talk about the basis of trigonometry, the unit circle. Draw a coordinate plane and only mark one unit in each direction.. Draw a circle that is centered at the origin and has a radius of one. This is the unit circle. Mark you x-axis and y-axis and also write cosine next to the x and sine n ...
FOG Unit 5 Circles - CMS Secondary Math Wiki
... Academic Tool: THINK ABOUT A PLAN – www.pearsonsuccessnet.com - Use Online Resource 12-3 Think About a Plan -OROn the CMS secondary wiki under Unit 5 resources – you will have access to download this file. (File name: 12-3 TAAP) http://secondarymath.cmswiki.wikispaces.net/Geometry Argumentation Task ...
... Academic Tool: THINK ABOUT A PLAN – www.pearsonsuccessnet.com - Use Online Resource 12-3 Think About a Plan -OROn the CMS secondary wiki under Unit 5 resources – you will have access to download this file. (File name: 12-3 TAAP) http://secondarymath.cmswiki.wikispaces.net/Geometry Argumentation Task ...
1.3 Trigonometric Functions
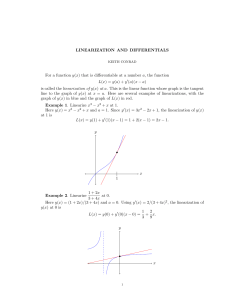
... Sign. It is very important to note that x and y in the definition above are not the lengths of the sides of a triangle, but the coordinates of the point P , which means that they are not necessarily positive. For example, if P projects onto the negative x-axis, the value of x is negative. As r is po ...
... Sign. It is very important to note that x and y in the definition above are not the lengths of the sides of a triangle, but the coordinates of the point P , which means that they are not necessarily positive. For example, if P projects onto the negative x-axis, the value of x is negative. As r is po ...
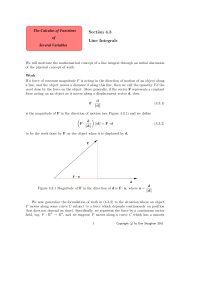
Section 4.3 Line Integrals - The Calculus of Functions of Several
... such that ϕ(s) = ψ(t) (such a value s has to exist since C is the image of both ψ and ϕ). Then g(t) = s. Proving that g is differentiable is not as easy, and we will not provide a proof here. However, assuming that g is differentiable, it follows that for any continuous ...
... such that ϕ(s) = ψ(t) (such a value s has to exist since C is the image of both ψ and ϕ). Then g(t) = s. Proving that g is differentiable is not as easy, and we will not provide a proof here. However, assuming that g is differentiable, it follows that for any continuous ...
Chapter 10 - Properties of Circles
... • If two chords intersect inside a circle, then the measure of each angle is one half the sum of the measures of the arcs intercepted by the angle and its vertical angle • Theorem 10.13 – Angles Outside Circle Theorem • If a tangent and a secant, two tangents, or two secants intersect outside a circ ...
... • If two chords intersect inside a circle, then the measure of each angle is one half the sum of the measures of the arcs intercepted by the angle and its vertical angle • Theorem 10.13 – Angles Outside Circle Theorem • If a tangent and a secant, two tangents, or two secants intersect outside a circ ...
Integral Tables and Integrals Using CAS
... Our textbook contains more than 100 integral patterns in a table (see Reference Pages 4 through 8 at the back of the book), a small number compared to reference books devoted solely to integral tables. Integral tables provide yet another way to help evaluate integrals. Using the tables, your goals s ...
... Our textbook contains more than 100 integral patterns in a table (see Reference Pages 4 through 8 at the back of the book), a small number compared to reference books devoted solely to integral tables. Integral tables provide yet another way to help evaluate integrals. Using the tables, your goals s ...
The Unit Organizer
... In the same circle, or in congruent circles, two minor arcs are congruent if and only if their corresponding chords are congruent. If one chord is a perpendicular bisector of another chord, then the first chord is a diameter. If a diameter of a circle is perpendicular to a chord, then the diameter b ...
... In the same circle, or in congruent circles, two minor arcs are congruent if and only if their corresponding chords are congruent. If one chord is a perpendicular bisector of another chord, then the first chord is a diameter. If a diameter of a circle is perpendicular to a chord, then the diameter b ...