Math 20B. Lecture Examples. Section 10.3. Convergence of series
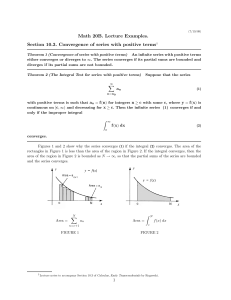
... Section 10.3. Convergence of series with positive terms† Theorem 1 (Convergence of series with positive terms) An infinite series with positive terms either converges or diverges to ∞. The series converges if its partial sums are bounded and diverges if its partial sums are not bounded. Theorem 2 (T ...
... Section 10.3. Convergence of series with positive terms† Theorem 1 (Convergence of series with positive terms) An infinite series with positive terms either converges or diverges to ∞. The series converges if its partial sums are bounded and diverges if its partial sums are not bounded. Theorem 2 (T ...
Developing the Calculus
... Observe that, using purely geometric methods, Barrow was able to arrive at this conclusion. He did not actually use the functional notation, nor did he realize the importance of the calculations that he was making. Therefore, it is not proper to say that Barrow invented Calculus. He merely stumbled ...
... Observe that, using purely geometric methods, Barrow was able to arrive at this conclusion. He did not actually use the functional notation, nor did he realize the importance of the calculations that he was making. Therefore, it is not proper to say that Barrow invented Calculus. He merely stumbled ...
sat math review
... The concepts covered on the SAT math sections include arithmetic and number theory, algebra and functions, geometry, and data analysis. You will not need to know matrices, logarithms, formal trigonometry, radians, standard deviation, or calculus. ...
... The concepts covered on the SAT math sections include arithmetic and number theory, algebra and functions, geometry, and data analysis. You will not need to know matrices, logarithms, formal trigonometry, radians, standard deviation, or calculus. ...
Section 6: Solving Right Triangles
... whenever such approximations are involved, we will round off all angles to the nearest hundredth of a degree, and all side lengths to four significant digits. Example 6.2 ---------------------------- -----------------------------------------------------------In each case, assume that right triangle ...
... whenever such approximations are involved, we will round off all angles to the nearest hundredth of a degree, and all side lengths to four significant digits. Example 6.2 ---------------------------- -----------------------------------------------------------In each case, assume that right triangle ...