Ch 2
... Combining these results, we see that the integral defining Γ(x) converges uniformly on [a, b], and the integrand is continuous in x and t. By an advanced calculus theorem, this makes Γ continuous on [a, b] and thus continuous at x0 . ♠ Exercise 2.1.1. Show that, for x real and positive, lim x Γ(x) ...
... Combining these results, we see that the integral defining Γ(x) converges uniformly on [a, b], and the integrand is continuous in x and t. By an advanced calculus theorem, this makes Γ continuous on [a, b] and thus continuous at x0 . ♠ Exercise 2.1.1. Show that, for x real and positive, lim x Γ(x) ...
Introduction Right
... As we want to apply arithmetic to complex numbers, we should allow all things of the form a + bi, where a and b are real numbers. This looks like a point, with coordinates (a, b). In the rush to introduce material, here is an idea whose time will come. The polar form of a complex number a + bi is an ...
... As we want to apply arithmetic to complex numbers, we should allow all things of the form a + bi, where a and b are real numbers. This looks like a point, with coordinates (a, b). In the rush to introduce material, here is an idea whose time will come. The polar form of a complex number a + bi is an ...
Unit 7 Circles - Clover Park School District
... Students continue to expand their understanding of geometry by exploring geometric relationships pertaining to circles. As was the case in algebra 1 and earlier in geometry, attributes of circles observed at earlier grades will now be looked at more precisely through proof. Many of the geometric rel ...
... Students continue to expand their understanding of geometry by exploring geometric relationships pertaining to circles. As was the case in algebra 1 and earlier in geometry, attributes of circles observed at earlier grades will now be looked at more precisely through proof. Many of the geometric rel ...
CIRCLES 10.1 Circles and Circumference CIRCLE
... 3. Then multiply the circumference of the circle by the ratio found in step 2. ...
... 3. Then multiply the circumference of the circle by the ratio found in step 2. ...
Precalculus Trigonometry Angles Remember: 360◦ = 2π radians
... The coordinates in the picture above are written to show a pattern: 20 , 21 , 22 , 23 , 24 . This pattern appears in both the x-coordinates and the y-coordinates (but the pattern goes one direction for the x-coordinates and the opposite direction for the y-coordinates). Some of these numbers are usu ...
... The coordinates in the picture above are written to show a pattern: 20 , 21 , 22 , 23 , 24 . This pattern appears in both the x-coordinates and the y-coordinates (but the pattern goes one direction for the x-coordinates and the opposite direction for the y-coordinates). Some of these numbers are usu ...
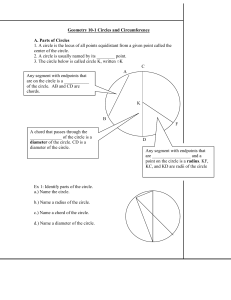
Geometry 10-1 Circles and Circumference A. Parts of Circles 1. A
... Ex 3: The diameters of d X , d Y , and d Z are 22 millimeters, 16 millimeters, and 10 millimeters respectively. a.) Find EZ. E ...
... Ex 3: The diameters of d X , d Y , and d Z are 22 millimeters, 16 millimeters, and 10 millimeters respectively. a.) Find EZ. E ...