Chapter 5: Poincare Models of Hyperbolic Geometry
... The fractional linear transformation, T , is usually represented by a 2 × 2 matrix ...
... The fractional linear transformation, T , is usually represented by a 2 × 2 matrix ...
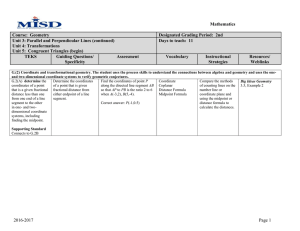
Geometry Chapter 3: Parallel and Perpendicular Lines Term Example
... Corresponding Angles - Angles that lie on the same side of the transversal t, on the same sides of lines r and s. Alternate Interior Angles - Nonadjacent angles that lie on opposite sides of the transversal t, between lines r and s. Alternate Exterior Angles – Angles that lie on opposite sides of th ...
... Corresponding Angles - Angles that lie on the same side of the transversal t, on the same sides of lines r and s. Alternate Interior Angles - Nonadjacent angles that lie on opposite sides of the transversal t, between lines r and s. Alternate Exterior Angles – Angles that lie on opposite sides of th ...
Axioms Corollaries
... Axiom 1: There is exactly one line through any two given points Axiom 2: [Ruler Axiom]: The properties of the distance between points. Axiom 3: Protractor Axiom (The properties of the degree measure of an angle). Axiom 4: Congruent triangles conditions (SSS, SAS, ASA) Axiom 5: Given any line l and a ...
... Axiom 1: There is exactly one line through any two given points Axiom 2: [Ruler Axiom]: The properties of the distance between points. Axiom 3: Protractor Axiom (The properties of the degree measure of an angle). Axiom 4: Congruent triangles conditions (SSS, SAS, ASA) Axiom 5: Given any line l and a ...
Three Dimensional Geometry
... 2. show that A (-1, -3, 4), B (7, -4, 7) and D (1, -6, 10 from a rhombus. 3. Find the direction cosines l, m, n of two lines which are connected by the relations l + m + n = 0 and mn – 2nl – 2lm = 0. 4. Lines OA, OB are drawn from O with direction cosines proportional to 1, -2, -1; 3, -2, 3. Find th ...
... 2. show that A (-1, -3, 4), B (7, -4, 7) and D (1, -6, 10 from a rhombus. 3. Find the direction cosines l, m, n of two lines which are connected by the relations l + m + n = 0 and mn – 2nl – 2lm = 0. 4. Lines OA, OB are drawn from O with direction cosines proportional to 1, -2, -1; 3, -2, 3. Find th ...
Honors Geometry Learning Outcomes
... The fundamental purpose of the course in Geometry is to formalize and extend students’ geometric experiences from the middle grades. Students explore more complex geometric situations and deepen their explanations of geometric relationships, moving towards formal mathematical arguments. Important di ...
... The fundamental purpose of the course in Geometry is to formalize and extend students’ geometric experiences from the middle grades. Students explore more complex geometric situations and deepen their explanations of geometric relationships, moving towards formal mathematical arguments. Important di ...
Bisector surfaces and circumscribed spheres of tetrahedra derived
... equidistant surfaces in Nil, SL 2 R and Sol geometries. In the Thurston spaces can be introduced in a natural way (see [8]) translations mapping each point to any point. Consider a unit vector at the origin. Translations, postulated at the beginning carry this vector to any point by its tangent mapp ...
... equidistant surfaces in Nil, SL 2 R and Sol geometries. In the Thurston spaces can be introduced in a natural way (see [8]) translations mapping each point to any point. Consider a unit vector at the origin. Translations, postulated at the beginning carry this vector to any point by its tangent mapp ...
Pacing
... given their equations G.G.64 Find the equation of a line, given a point on the line and the equation of a line perpendicular to the given line G.G.65 Find the equation of a line, given a point on the line and the equation of a line parallel to the desired line G.G.70 Solve systems of equations invol ...
... given their equations G.G.64 Find the equation of a line, given a point on the line and the equation of a line perpendicular to the given line G.G.65 Find the equation of a line, given a point on the line and the equation of a line parallel to the desired line G.G.70 Solve systems of equations invol ...
End of Module Study Guide: Concepts of Congruence Rigid Motions
... Alternate Interior Angles: Angles on opposite sides of the transversal on the inside of the parallel lines. Alternate interior angles are congruent because you can map one to another by rotating 180° arou ...
... Alternate Interior Angles: Angles on opposite sides of the transversal on the inside of the parallel lines. Alternate interior angles are congruent because you can map one to another by rotating 180° arou ...
Parallel Lines and Transversals
... Parallel Lines and Transversals Two lines divide the plane into three regions. The region between the lines is referred to as the interior. The two regions not between the lines is referred to as the exterior. ...
... Parallel Lines and Transversals Two lines divide the plane into three regions. The region between the lines is referred to as the interior. The two regions not between the lines is referred to as the exterior. ...
Math 3329-Uniform Geometries — Lecture 13 1. A model for
... clear which geometry Riemann actually had in mind. From Riemann’s point of view, in fact, they are simply different spaces with the same geometry, so he may have actually been talking about both. 2. The Models for Elliptic Geometry Axioms will begin fade into the background for us now, and what a sy ...
... clear which geometry Riemann actually had in mind. From Riemann’s point of view, in fact, they are simply different spaces with the same geometry, so he may have actually been talking about both. 2. The Models for Elliptic Geometry Axioms will begin fade into the background for us now, and what a sy ...
Riemannian connection on a surface

For the classical approach to the geometry of surfaces, see Differential geometry of surfaces.In mathematics, the Riemannian connection on a surface or Riemannian 2-manifold refers to several intrinsic geometric structures discovered by Tullio Levi-Civita, Élie Cartan and Hermann Weyl in the early part of the twentieth century: parallel transport, covariant derivative and connection form . These concepts were put in their final form using the language of principal bundles only in the 1950s. The classical nineteenth century approach to the differential geometry of surfaces, due in large part to Carl Friedrich Gauss, has been reworked in this modern framework, which provides the natural setting for the classical theory of the moving frame as well as the Riemannian geometry of higher-dimensional Riemannian manifolds. This account is intended as an introduction to the theory of connections.