* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download File
Riemannian connection on a surface wikipedia , lookup
Trigonometric functions wikipedia , lookup
Problem of Apollonius wikipedia , lookup
History of trigonometry wikipedia , lookup
System of polynomial equations wikipedia , lookup
Line (geometry) wikipedia , lookup
Analytic geometry wikipedia , lookup
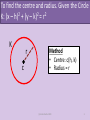
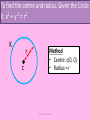
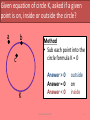
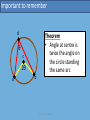
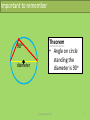
Co-ordinate Geometry of the Circle Notes Aidan Roche 2009 (c) Aidan Roche 2009 1 Given the centre and radius of a circle, to find the equation of Circle K? K r c(h, k) Method • Sub centre & radius into: (x – h)2 + (y – k)2 = r2 • If required expand to: x2 + y2 +2gx +2fy + c = 0 (c) Aidan Roche 2009 2 To find the centre and radius. Given the Circle K: (x – h)2 + (y – k)2 = r2 K r c Method • Centre: c(h, k) • Radius = r (c) Aidan Roche 2009 3 To find the centre and radius. Given the Circle K: x2 + y 2 = r2 K r c Method • Centre: c(0, 0) • Radius = r (c) Aidan Roche 2009 4 To find centre and radius of K. Given the circle K: x2 + y2 +2gx +2fy + c = 0? K r c Method • Centre: c(-g, -f) 2 2 r g f c • Radius: (c) Aidan Roche 2009 5 Given equation of circle K, asked if a given point is on, inside or outside the circle? a b c K Method • Sub each point into the circle formula K = 0 Answer > 0 Answer = 0 Answer < 0 (c) Aidan Roche 2009 outside on inside 6 Important to remember d Theorem • Angle at centre is twice the angle on the circle standing the same arc θ c 2θ a b (c) Aidan Roche 2009 7 Important to remember 90o diameter Theorem • Angle on circle standing the diameter is 90o (c) Aidan Roche 2009 8 To find equation of circle K given end points of diameter? K a c r b Method • Centre is midpoint [ab] • Radius is ½|ab| • Sub into circle formula (c) Aidan Roche 2009 9 To prove a locus is a circle? Method • r c K • If the locus of a set of points is a circle it can be written in the form: x2 + y2 +2gx + 2fy + c = 0 We then can write its centre and radius. (c) Aidan Roche 2009 10 To find the Cartesian equation of a circle given Trigonometric Parametric equations? Method • Trigonometric equations of a circle are always in the form: x = h ± rcosѲ y = k ± rsinѲ • Sub h, k and r into Cartesian equation: (x – h)2 + (y – k)2 = r2 r c K (c) Aidan Roche 2009 11 To prove that given Trigonometric Parametric equations (x = h ± rcosѲ, y = k ± rsinѲ) represent a circle? Method r c K • • • • Rewrite cosѲ (in terms of x, h & r) and then evaluate cos2Ѳ. Rewrite sinѲ (in terms of y, h & r) and then evaluate sin2Ѳ. Sub into: sin2Ѳ + cos2Ѳ = 1 If it’s a circle this can be written in the form: x2 + y2 +2gx + 2fy + c = 0 (c) Aidan Roche 2009 12 To find the Cartesian equation of circle (in the form: x2 + y2 = k) given algebraic parametric equations? Method r c • Evaluate: x2 + y2 • The answer = r2 • Centre = (0,0) & radius = r K (c) Aidan Roche 2009 13 Given equations of Circle K and Circle C, to show that they touch internally? C r1 K c1 r2 c2 d Method • Find distance between centres • If d = r1 - r2 QED (c) Aidan Roche 2009 14 Given equations of Circle K and Circle C, to show that they touch externally? C K r1 r2 d c2 Method • Find distance d between centres • If d = r1 + r2 QED c1 (c) Aidan Roche 2009 15 Given circle K and the line L to find points of intersection? b L Method • Solve simultaneous equations a K (c) Aidan Roche 2009 16 Important to remember K 90o t radius c Theorem • A line from the centre (c) to the point of tangency (t) is perpendicular to the tangent. Tangent (c) Aidan Roche 2009 17 Important to remember b d a radius 90o c Theorem • A line from the centre perpendicular to a chord bisects the chord. (c) Aidan Roche 2009 18 Given equation of Circle K and equation of Tangent T, find the point of intersection? T K t Method • Solve the simultaneous equations (c) Aidan Roche 2009 19 Given equation of Circle K and asked to find equation of tangent T at given point t? T Method 1 • Find slope [ct] • Find perpendicular slope of T • Solve equation of the line t c Method 2 K • Use formula in log tables (c) Aidan Roche 2009 20 To find equation of circle K, given that x-axis is tangent to K, and centre c(-f, -g) ? Method K c(-g, -f) • On x-axis, y = 0 so t is (-f, 0) • r = |f| • Sub into circle formula r = |f| X-axis t(-g, 0) (c) Aidan Roche 2009 21 To find equation of circle K, given that y-axis is tangent to K, and centre c(-f, -g) ? r = |g| t(0, -f) y-axis c(-g, -f) Method • On y-axis, x = 0 so t is (0, -g) • r = |g| • Sub into circle formula K (c) Aidan Roche 2009 22 Given equation of Circle K and equation of line L, how do you prove that L is a tangent? Method 1 L K r • Solve simultaneous equations and find that there is only one solution Method 2 c • Find distance from c to L a ( g ) b( f ) c d a 2 b2 • If d = r it is a tangent (c) Aidan Roche 2009 23 Given equation of Circle K & Line L: ax + by + c = 0 to find equation of tangents parallel to L? L Method 1 T1 r c K • Find centre c and radius r • Let parallel tangents be: ax + by + k = 0 • Sub into distance from point to line formula and solve: a ( g ) b( f ) k r a 2 b2 r T2 (c) Aidan Roche 2009 24 Given equation of Circle K and point p, to find distance d from a to point of tangency? Method T • Find r • Find |cp| • Use Pythagoras to find d t d? r c |cp| p K (c) Aidan Roche 2009 25 Given equation of Circle K and point p, to find equations of tangents from p(x1,y1)? T1 Method 1 r K c r T2 p • Find centre c and radius r • Sub p into line formula and write in form T=0 giving: mx – y + (mx1 – y1) = 0 • Use distance from point to line formula and solve for m: m ( f ) 1( g ) ( mx1 y1 ) r m 2 12 (c) Aidan Roche 2009 26 Given equation of Circle K and Circle C, to find the common Tangent T? T C Method • Equation of T is: K–C=0 K (c) Aidan Roche 2009 27 Given equation of Circle K and Circle C, to find the common chord L? L Method • Equation of T is: K–C=0 K C (c) Aidan Roche 2009 28 Given three points and asked to find the equation of the circle containing them? b a Method • Sub each point into formula: x2 + y2 + 2gx + 2fy + c = 0 • Solve the 3 equations to find: g, f and c, • Sub into circle formula c (c) Aidan Roche 2009 29 Given 2 points on circle and the line L containing the centre, to find the equation of the circle? b a Method • Sub each point into the circle: x2 + y2 + 2gx + 2fy + c = 0 • Sub (-g, -f) into equation of L • Solve 3 equations to find: g, f and c, • Sub solutions into circle equation L (c) Aidan Roche 2009 30 Given the equation of a tangent, the point of tangency and one other point on the circle, to find the equation of the circle? L a Method b T • Sub each point into the circle: x2 + y2 + 2gx + 2fy + c = 0 • Use the tangent & tangent point to find the line L containing the centre. • Sub (-g, -f) into equation of L • Solve 3 equations to find: g, f and c, • Sub solutions into circle equation (c) Aidan Roche 2009 31